Estudio comparativo de la eficiencia y eficacia frente al uso de algoritmos genéticos y de enjambres1

Resumen

Este artículo se enfoca en el análisis comparativo entre la eficiencia y la eficacia de dos técnicas de búsquedas, con la intención de evaluar el comportamiento en el ajuste de soluciones. Las dos técnicas analizadas son los algoritmos genéticos y el enjambre de partículas. Ambas han demostrado ser efectivas y su aplicación abarca problemas en muy diversas áreas. Sus estructuras han probado ser capaces de resolver de forma eficiente problemas de búsquedas no informadas en sistemas complejos; además, se caracterizan por sus poblaciones de coeficientes estáticos, preprogramados y adaptativos. Siendo así, el objetivo principal es enfocar las dos técnicas y encontrar cuál de las dos se aproxima de mejor manera a un conjunto de medidas experimentales, así como analizar las similitudes y diferencias entre dichas técnicas de optimización. La optimización consiste en encontrar aquellos valores en el espacio de búsqueda que representan una solución cercana para un problema dado. El planteamiento inicial considera la evaluación sobre un diseño numérico de optimización las cuales sirven de modelo para determinar el comportamiento, incluso frente a técnicas de ajustes tradicionales; sin embargo, no se pretende calificar como mejor alguna de las dos técnicas, sino dar elementos que permitan decidir cuál de ellas utilizar ante un problema de características similares al caso de estudio planteado. Por tal motivo, al realizar el estudio pertinente, se demostró que los algoritmos genéticos son métodos con estructuras que implementan un mecanismo de adaptación y pueden seguir solucionándolo.

Palabras clave: comportamiento, algoritmos, espacio de búsqueda, coe- ficientes estáticos, adaptativos, parámetros, medidas experimentales, análisis, optimización.

I. INTRODUCCIÓN

Actualmente los algoritmos intentan encontrar las mejores soluciones en un espacio de búsqueda; sin embargo, los desarrolladores de estos se han dado cuenta de que estos no son factibles para esa función, sino que son esenciales para obtener una solución cercana a la óptima [1]. En consecuencia, cada punto en el espacio de búsqueda tiene asociado un valor numérico denominado valor de adaptación [2].

Las personas que trabajan en ciencia y tecnología a me- nudo se enfrentan a la necesidad de elegir entre diferen- tes soluciones posibles para un problema determinado, con el objetivo de lograr resultados relevantes [3]. La optimización es el proceso de tomar estas decisiones de la mejor manera posible [4]. Los resultados relevantes hacen referencia a encontrar las mejores soluciones a un problema. Así, en un problema de optimización, se comparan y contrastan soluciones candidatas, lo que in- dica que la calidad de las soluciones es muy importante [5]. En ese sentido, la mejor solución generalmente viene dada por el punto en el espacio de búsqueda que se asocia con el valor de coincidencia más alto, pero hay trabajos donde el valor de coincidencia se puede visualizar como el valor de error asociado a cada punto del espacio. En tales casos, la mejor solución viene dada por el punto del espacio que tiene el mínimo error asociado y, por tanto, el valor mínimo del ajuste.

Se define como algoritmo aquella serie de pasos que describen un proceso de búsqueda de una solución de un problema concreto, a este problema se le añade una optimización para encontrar aquellos valores en el espacio de búsqueda que representen la mejor solución [6].

Los algoritmos genéticos son aquellas técnicas inspiradas en la reproducción de los seres vivos y que imitan a la evolución biológica y en la idea de que el que sobrevive es el que está mejor adaptado al medio [7]. Charles Darwin fue el primero que dispuso la teoría evolutiva en su libro Origen de las especies, publicado en 1859, en el cual se inspira la evolución biológica darwiniana [8].

Por otra parte, los algoritmos de enjambre son aquellos mecanismos que enfatizan en el estudio de los sistemas informáticos inspirado en la inteligencia colectiva [9], que resulta de la cooperación de un gran número de factores similares en el entorno. Algunos ejemplos son los bancos de peces o de aves y las colonias de hormigas [10]. Esta inteligencia es descentralizada, autoorganizada y distribuida localmente. En la naturaleza, estos sistemas

se utilizan a menudo para resolver problemas como la búsqueda de alimento eficiente, la evitación de depre- dadores o el movimiento de colonias [11].

El uso de algoritmos evolutivos en problemas de opti- mización ha sido intenso durante la última década. El estudio de un algoritmo es un proceso iterativo que trabaja sobre un conjunto de P individuos para formar una población y aplicarle un conjunto de operadores variacionales, lo que permite constituir una evolución y mejora de grupos de individuos, esto es, una medida de cuán buena o mala es la solución propuesta por un individuo para un problema dado. Estos algoritmos se utilizan a menudo para resolver problemas complejos, como tareas de optimización.

El comportamiento que muestra un estudio de aplicación al resolver problemas está determinado por el equilibrio que preserva mediante la manipulación de soluciones de población entre la observación local de las mejores soluciones y la exploración del campo de investigación.

Si un estudio de aplicación tiene una alta capacidad de utilización, los individuos (soluciones potenciales) evolucionarán muy rápidamente hacia las mejores soluciones cercanas en el espacio de búsqueda, que, muy probablemente, no serán soluciones óptimas al problema, y será muy difícil escapar.

La consecuencia de este rápido progreso de las soluciones convoca una fuerte pérdida de diversidad en la población (todas las soluciones que la componen se vuelven muy similares), por lo que la evolución de los individuos se detiene (es decir, los operadores de variación no pueden generar mejores individuos que los existentes).

Por el contrario, un algoritmo que faculta demasiado escaneo cubrirá una parte muy amplia del espacio de búsqueda, pero no podrá profundizar en las áreas más prometedoras, por lo que no encontrará soluciones de calidad.

En general, la solución del problema de optimización dada por el punto en el espacio de búsqueda con el valor de aptitud más pequeño o más grande no es fácil de encontrar, ya sea porque se encuentra en un espacio de búsqueda grande o por las adaptaciones asociadas a él. En la práctica, este tipo de problemas son difíciles de resolver, debido a la imposibilidad de probar y comparar cada una de las posibles soluciones para encontrar la solución óptima en un tiempo aceptable.

En problemas con un espacio de solución pequeño, se pueden buscar todas las soluciones posibles y encontrar la óptima entre ellas. Sin embargo, en problemas con grandes espacios de solución, se vuelve poco práctico utilizar algoritmos deterministas como fuerza bruta o símplex, y no hay garantía de una solución óptima en un tiempo razonable. En tales problemas, el espacio de búsqueda a menudo no solo es muy grande, sino también discontinuo o ruidoso, lo que dificulta encontrar la solución óptima.

Finalmente, en la mayoría de estos problemas no se requiere encontrar la solución global absoluta, sino alguna solución o conjunto de soluciones que correspondan a un valor inferior a alguna función objetivo. Esto es, que las soluciones encontradas sean indicadas. Debido a ello, en los últimos años se enfatizó el uso de técnicas de búsqueda aproximadas para resolver problemas de optimización, porque estas pueden encontrar soluciones cercanas a la óptima en un tiempo de cómputo aceptable. Aunque se han desarrollado diversas y muy variadas técnicas de búsqueda aproximada, en este artículo abordaremos solo dos de las más utilizadas en la optimización por enjambres de partículas.

Además, se utilizarán estos dos algoritmos en una opti- mización de programación MATLAB, enfocados así: para el algoritmo genético, tres operadores: selección, cruce y mutación; para el algoritmo de enjambre: conocimiento sobre el entorno, conocimiento histórico y experiencias de los individuos cercanos.

II. FASES DE ALGORITMO

A. Fase 1. Percepción del algoritmo genético simple

Los algoritmos genéticos son formas y métodos basados en el proceso natural de los organismos, en los cuales los miembros de una población dada compiten entre sí, lo que hace que esos individuos tengan más probabilidades de producir un gran número de descendientes, y que el talento del grupo se reduzca en un número menor, en el sentido de que los individuos mejor adaptados a su entorno tienen más probabilidades de dejar pasar o reproducirse en descendencia. Su descendencia (hijos) adopta y tiene esta adaptación y un mayor porcentaje de posibilidades reproductivas que los padres. Así, las especies que logran desarrollar rasgos cada vez más avanzados evolucionan, dependiendo de su entorno y de su historia evolutiva genética.

La evolución se entiende como un proceso reactivo en el que un organismo continúa desarrollándose, teniendo en cuenta el entorno. Vale la pena recordar la teoría de la evolución biológica de mediados del siglo XIX, que se basó en la teoría de la selección natural de Darwin (1859) y el trabajo de Mendel sobre la herencia (1865) [12]. Charles Darwin introdujo el mecanismo de la selección natural en 1859 como una forma de explicar las propiedades de los organismos, que hoy en día pueden ser tan complejos dada la forma en que se han desarrollado a lo largo de su historia: “La evolución se puede definir como una descendencia modificada” [13], si la analizamos como un fenómeno que consiste en la consolidación y unificación de la biología. Esta selección es un proceso que se da, precisamente, cuando hay variación fenotípica entre los individuos, en parte una degeneración. Es hereditario, así que hay una relación causal (probabilidad) entre esta variación y el éxito reproductivo de un individuo [14].

Otro aspecto a detallar sobre la teoría de la evolución genética de Charles Darwin son las diferencias entre animales y plantas de una misma especie, pues, aunque nos parezca increíble, son los ejemplares que mejor se adaptan a la lucha por la supervivencia y transmiten sus rasgos físicos, fisiológicos y cognitivos a su descendencia. También podemos llamar a este rasgo de herencia selección natural, por el cual los miembros de una determinada población evitan la extinción de su propia especie.

Por otro lado, está el énfasis de los hallazgos genéticos, como los del monje austríaco Gregory Mendel, quien des- cubrió que los patrones de herencia pueden ser fácil- mente el resultado de genes individuales, así como las leyes de probabilidad y estadísticas de los mismos. Gracias a ello, Mendel estableció los cruces de reproducción entre plantas, basado en lo que consideró como heredar las características de un organismo progenitor a la descendencia.

B. Fase 2. Aplicación de los principios del algoritmo genético

Los algoritmos genéticos simples fueron introducidos por primera vez como algoritmos de búsqueda, utilizando la metáfora de la población genética en la comunidad de algoritmos genéticos, ya que el problema de optimización se desplazó al mejor ajuste de los individuos [15]. A esto lo llamamos cromosoma en una población, y se mide mediante una función de aptitud, o función de ajuste, relacionada con la función cognitiva del problema que se está resolviendo. Los algoritmos genéticos actúan sobre la población modificando sus propiedades. Se establece qué los principios básicos de los algoritmos genéticos

correspondientes a las leyes naturales de la vida des- critas por Darwin, imitan los principios de la vida y utilizándolos para optimizar objetivos:

• Existe una población de personas con diferentes características y capacidades.

• Existe un límite en el número de individuos que pueden existir en una población determinada.

• La naturaleza crea nuevos individuos con caracte- rísticas similares a los existentes.

• Los individuos más prometedores suelen reproducirse por selección natural.

Su aplicación se realiza mediante la codificación y la decodificación, de la siguiente manera:

Se determina la parte entera de la relación del valor del individuo con respecto a un valor máximo mediante la expresión:

[:]

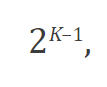donde K corresponde al número de iteraciones.

Luego, para el proceso de decodificación, se toma el valor decimal a partir de una expresión binaria:

[:]

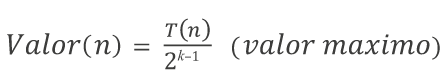donde es el número de individuos de una generación.

Ahora bien, un individuo puede representarse como un conjunto de parámetros (genes), que son divisiones con- ceptuales de genes en los que codifican algún tipo de rasgo. Los colores de los ojos, cuando se combinan para formar un conjunto de valores, comúnmente llamados cromosomas, deben tener suficientes representaciones de genes para usarlos más tarde en un algoritmo genético y asignarles algún valor. Para este, se consideran 3 tipos simples de representaciones de genes:

• Binario: utilizando un vector cuya longitud es el número de genes por organismo, el valor que se puede obtener de cada elemento es un número binario.

• Entero: utiliza un vector cuya longitud es igual al número de genes del individuo, y el valor que se puede tomar de cada elemento es un número entero.

• Real: se emplea un vector cuya longitud es el número de genes por individuo y cuyo valor se puede tomar de cada elemento que se convierte en un número real.

C. Fase 3. Evaluación del algoritmo genético

Los tres algoritmos genéticos descritos en esta sección fueron introducidos por de Jong (1975) y se basan en los siguientes parámetros:

• La evaluación de rendimiento, que mide el rendimiento promedio de todos los subprocesos generados en el momento T.

• La evaluación offline, sobre cómo utilizar algoritmos genéticos en el proceso de combinación óptima.

• La mejor clasificación.

D. Fase 4. Percepción del algoritmo de enjambre

El algoritmo por enjambre de partículas, conocido como algoritmo de enjambre, se ha caracteriza por su eficiencia y bajo costo computacional. Además, se orienta a encon- trar mínimos o máximos globales y su comportamiento se dirige hacia factores de dirección, velocidad y aceleración, como resultado de combinar las decisiones individuales de cada uno con el comportamiento del resto [16].

Los elementos principales que componen el algoritmo de enjambre son tres [17]:

1. El control de la congestión, que consiste en responder a sobrecargas de la red.

2. La seguridad de la comunicación, que consiste en la unión que accede de forma inteligible la información.

3. El enrutamiento, que consiste en llevar el proceso de selección de una ruta a través de una o más redes.

Este algoritmo se encuentra enfocado en el comporta- miento social de los seres vivos y lo asociaron con com- portamientos colectivos de varios grupos de animales como son los peces, manadas, entre otros, para describir los factores estándar a los que este algoritmo se acopla. Su descripción es cognitiva, pues esta contribuye para que el valor numérico tenga una especie de memoria y pueda saber si anteriormente había adoptado una posi- ción [18]. El algoritmo tiene dos subdominios importantes que categorizan la partícula: la optimización del grupo como objeto de estudio y la optimización probabilística a través de la computación evolutiva [19].

Se dice que los algoritmos de enjambre toman como referencia el modelo gbest, que consiste en que las partículas tengan una comunicación concreta e interre- lacionada, con el fin de encontrar un valor óptimo. Otro modelo es el lbest, que evita una convergencia prematura y mantiene varios puntos de atracción [20].

E. Fase 5. Evaluación del algoritmo de enjambre de partículas

Para observar la correspondencia ideal para el algoritmo de enjambre, se han dispuesto topologías de los modelos gbest y lbest para generar un valor óptimo para la optimización de la búsqueda y sus dominios, de esta manera, se establecen [21]:

• La inercia como la influencia de otros.

• La constricción como el equilibrio entre búsquedas locales y globales.

• La inercia modulada como la disminución de variables incontrolables.

III. OPTIMIZACIÓN DE LOS ALGORITMOS A TRAVÉS DEL PROGRAMA MATLAB

A. Aplicación de los algoritmos a través de MATLAB

Para proporcionar una solución de problemas de máxi- mos múltiples, mínimos múltiples y optimización no dife- renciables con estos algoritmos es esencial utilizar un programa que permita obtener la búsqueda de patrones de algún grupo colectivo. Por tanto, se consideró utilizar el conjunto de herramientas Global Optimization Toolbox, que permite buscar soluciones globales a problemas que contienen máximos y mínimos múltiples, además de ofrecer solvers (solucionadores) de sustituto, búsqueda de patrones, algoritmo genético, enjambre de partículas, recocido simulado, multiarranque y búsqueda global. Sus técnicas de optimización convierten la descripción de un problema en una expresión matemática, para luego llegar una solución eficiente y precisa a este problema; ademas, el problema depende de las características de la función objetivo y restricciones.

En cuanto al algoritmo genético, lo que hace esta herramienta es especificar el solver y darle una tarea al

optimize (optimizador) de live editor (editor en cuestión) para darle un enfoque basado en el problema a resolver y luego, establecer criterios de paradas aplicables al solver seleccionado [22].

Mientras que, para el algoritmo de enjambre, se utiliza la función solver GlobalSearch y Multistart, con el objetivo de aplicar gradientes a la localización de los mínimos lo- cales a partir de varios puntos de arranque en la búsqueda de mínimos globales. Luego, se hace una optimización de sustituto con restricciones no lineales.

B. Búsqueda de patrones a través de estos algoritmos

Para hallar una solución de problema de optimización mediante el uso de funciones MATLAB, es fundamental ubicar los patrones deseados, por tanto, se realiza una búsqueda directa.

En el caso del algoritmo genético, es necesario utilizar la búsqueda de patrones generalizados (GPS), en la cual se realizan opciones de sondeo, se establece el número de puntos que evaluar en cada paso y se utiliza un paso de búsqueda opcional para aumentar la eficiencia y contro- lar la forma en que cambia la malla [23]. El algoritmo genético, una vez aplicado a esta búsqueda, identificará los mínimos globales, imitando los principios de la evolución biológica, modificando una población de puntos indivi- duales mediante reglas de los modelos combinacionales genéticos en la reproducción biológica.

Por otra parte, el enjambre de partículas también buscara los mínimos globales mediante un algoritmo basado en el comportamiento de los enjambres de un grupo selec- tivo, como los de peces o moscas, por ejemplo. Como el enjambre hace relación a un grupo, a este mismo se le identificara como partícula, con el objetivo de determinar su velocidad y dirección para hallar la mejor ubicación hasta el momento. Una vez aplicado el algoritmo de enjambre de partícula a toda su búsqueda, se configura la velocidad de cálculo, mediante el establecimiento de ponderaciones de ajuste social, autoajuste y ajuste de inercia.

A continuación, en la figura 1 y figura 2 (Variaciones del algoritmo genético ante mediciones experimentales respecto a una misma respuesta [19]) se mostrará el comportamiento de cada algoritmo cuando entra en su búsqueda de optimización.

Figura 1.
Variaciones del algoritmo genético ante mediciones experimentales respecto a una misma respuesta
Tomada de [19].

Figura 1.
Variaciones del algoritmo genético ante mediciones experimentales respecto a una misma respuesta
Tomada de [19].

Figura 2.
Variaciones del algoritmo genético ante mediciones experimentales respecto a una misma respuesta
Tomada de [19].

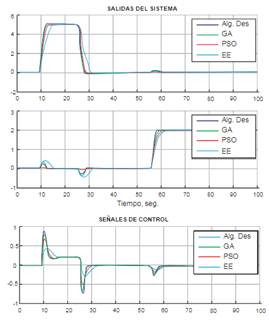
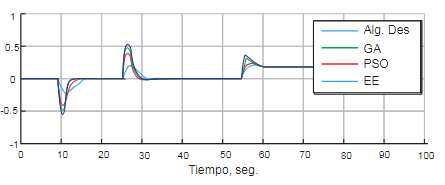
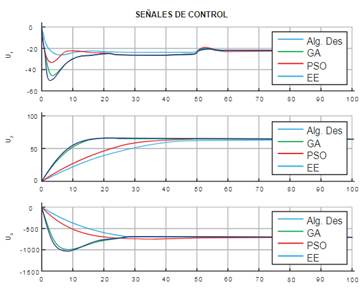
Métodos de optimización

Para iniciar se exponen los aspectos como la analogía con la naturaleza, la configuración de los parámetros y el pseudocódigo. Luego, se describe la implementación en funciones matemáticas multivariable, para verificar el correcto desempeño de cada técnica y finalmente, se analiza el desempeño de las técnicas y se presentan las discusiones acerca de su implementación en funciones matemáticas multivariable.

1. Optimización mediante enjambre de partículas (PSO)

Las partículas recorren distintas posiciones en el área de soluciones, según el movimiento del enjambre, teniendo presente la mejor posición individual y grupal [24].

El algoritmo asigna cada partícula como una posición definida a un punto en un espacio de D dimensiones. Cada partícula ajusta su vuelo mediante la ecuación de actualización de velocidad, según Shi y Eberhart [25].

La ecuación de actualización de posición para cada partícula está definida así:

[:]

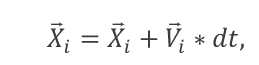donde dt Importar imagen corresponde al radio de avance, que permite mantener las partículas dentro del espacio de búsqueda predeterminado; Importar imagen es el vector velocidad de la i-ésima partícula, y Importar imagen es el vector posición de la i-ésima partícula.

[:]

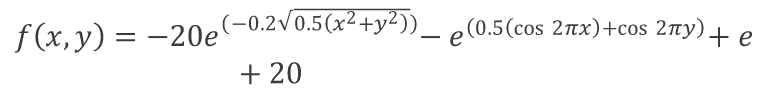Función Step. Es una representación discretizada de la función Esfera, donde entero es una función que aproxima al entero más cercano. Por tal razón, se considera con un nivel de complejidad bajo. El reto que quizás puede ofrecer se atribuye al hecho de que el enjambre debe reconocer muy bien el espacio de solución y tener la ca- pacidad de, progresivamente, ir transitando hacia las zonas con menor amplitud, hasta llegar al punto de interés:

[:]

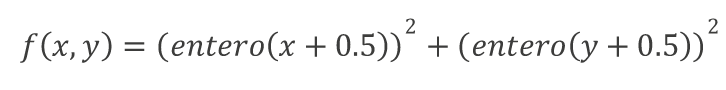Función de Rosenbrock. Se puede considerar como una función con un nivel de complejidad intermedio. El reto que ofrece corresponde a la precisión que se debe tener para llegar al punto exacto de interés sin converger prematuramente a causa de no evidenciar un cambio notorio en amplitud en los puntos de la planicie y de la zona más baja del espacio de solución:

[:]

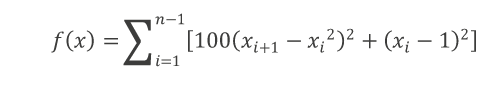El mínimo de cada función se calculó con el fin de caracterizar el comportamiento del algoritmo.

Análogamente, solo se varió un parámetro, dejando a los demás fijos, con datos recomendados en [26], [27] y [28].

c) Análisis de resultados PSO

La implementación de los algoritmos se hizo sobre un conjunto de funciones multivariables, con el fin de poner a prueba su funcionamiento y, a partir de su evaluación, se caracterizó el comportamiento de los mismos frente a los distintos retos que las funciones ofrecen.

El comportamiento del algoritmo de optimización me- diante enjambre de partículas por medio de las imple- mentaciones sugiere que el número de partículas sea de 30, puesto que ubicar más partículas dentro del es- pacio mejora la búsqueda del mínimo global. De igual manera, el número de iteraciones no debe ser un límite que interrumpa el avance de las partículas, por lo cual se propone que el valor de este parámetro sea mayor de 20 iteraciones, teniendo en cuenta que se desconoce el momento en que el enjambre convergerá al mínimo global.

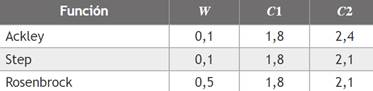
En cuanto al valor del peso de inercia y las constantes exploratorias, se presentaron distintos valores para cada función de prueba. Sin embargo, los valores más destacados correspondieron a un peso de inercia de Importar imagen , y constantes globales y locales en el rango de 0,1 a 2,6. La variación de estos parámetros influyó en el comportamiento del enjambre ante distintas funciones de prueba.

En cuanto al valor del peso de inercia y las constantes exploratorias, se presentaron distintos valores para cada función de prueba. Sin embargo, los valores más destacados correspondieron a un peso de inercia de 0,5 (W=0,5)

y constantes globales y locales en el rango de 0,1 a 2,6. La variación de estos parámetros influyó en el comportamiento del enjambre ante distintas funciones de prueba.

El valor en el delta de tiempo que arrojó mejores resul- tados para todas las funciones en pruebas preliminares fue de

En la tabla 1 se presentan los resultados obtenidos para el número de partículas (np), el peso de inercia ( w ) y las constantes de exploración local y global c1 y c2, respectivamente.

Tabla 1.
Resultados para cada función
Elaboración propia.

(1) Ventajas del algoritmo PSO

• Facilidad en la implementación, dado que se manejan pocos parámetros y tan solo existen dos ecuaciones de actualización, que corresponden a la velocidad y la posición de cada partícula.

• Permite el ajuste directo en la característica de la búsqueda que se quiere realizar, por medio de la asignación de valores en las constantes c1 y c2.

• Por ser un algoritmo de enjambre, facilita la visua- lización del comportamiento del mismo frente a los retos que una función le puede ofrecer.

(2) Desventajas del algoritmo PSO

· En vista de que el comportamiento del enjambre es sensible a cambios en los valores de los parámetros, el mal manejo de estos valores puede ocasionar una convergencia prematura.

· En el caso de funciones multivariables, es necesario conocer el rango del espacio de solución, de modo que el radio de avance que experimenta cada par- tícula esté dentro de ese espacio. De lo contrario, la búsqueda no se encaminará dentro de las fronteras, sino fuera de ellas.

d) Discusión

A partir de los resultados registrados para el esquema de pruebas propuesto, se evidencia que el peso de inercia es un factor que influye en la capacidad de exploración de las partículas, en la cantidad de iteraciones necesarias para la obtención del mínimo global y en la velocidad con que las partículas se mueven dentro del espacio solución. El aumento en el peso de inercia conlleva un aumento en el número de iteraciones.

Importar imagen Otro parámetro que afecta la velocidad con que las partículas se desplazan en el espacio de solución es el radio de avance. Se recomienda usar un valor de Importar imagen , que permita a las partículas realizar una actualización equilibrada con respecto al área explorada del espacio de solución.

En cuanto a las constantes c1 y c2, los resultados de las pruebas efectuadas indican que estas constantes afectan la comunicación entre partículas y, por ende, se afecta la orientación de las mismas hacia la obtención del mínimo global. Por consiguiente, es mejor asignar un mayor peso a la búsqueda global con respecto a la búsqueda local, con el objetivo de reconocer el espacio de solución y permitir una búsqueda de largo alcance.

1. Optimización mediante algoritmos genéticos (GA)

Este esquema permite agrupar una lista de caracterís- ticas de cada individuo, en una cadena que representa mediante parámetros estas características. Los indivi- duos son seleccionados de acuerdo con su mayor nivel de aptitud, mediante el uso de una función de adaptación. Esta función determina qué modelos presentan las me- jores características según el requerimiento del pro- blema bajo consideración. Una vez que se han escogido los pares de mejores individuos, se aplican las operaciones que facilitan el surgimiento de nuevos individuos cuyos

valores de aptitud sean mejores que los obtenidos por sus antecesores. Aquellos individuos cuyos valores de aptitud se consideren bajos son descartados definiti- vamente, según lo consultado en [29].

La función de adaptación evalúa a cada individuo de la generación anterior, determinando su nivel de aptitud para seleccionar a los dos mejores individuos. Una vez escogidos los individuos caracterizados por su mejor aptitud, se someten a los procesos de cruce y mutación. Estos procesos producen una nueva generación de indi- viduos que repiten el ciclo de evaluación, mientras que aquellos menos aptos de la generación anterior se descartan.

a) Funciones multivariables

Para los algoritmos genéticos, es necesario contar con un tamaño de población grande, que permita obtener una mayor información del espacio de solución. Respecto a la tasa de cruce, es común que las nuevas generaciones conservan rasgos característicos de generaciones pa- sadas; por esta razón, la tasa de cruce es alta. En cuanto a la tasa de mutación, se considera que es necesario tenerla en cuenta, pero como un caso aislado, debido a que en la naturaleza el fenómeno de mutación es poco común. En consecuencia, la tasa de mutación es baja.

b) Análisis de resultados GA

El análisis de la variación de parámetros como el nú- mero de individuos y las tasas de cruce y mutación, no representan un impacto en el comportamiento que presentan los individuos a lo largo de las generaciones. Por tanto, el análisis de la variación de estos parámetros se enfoca en la precisión del mínimo global de la función objetivo encontrado y en las iteraciones realizadas para encontrar dicho punto.

El mejor tamaño de la población para el algoritmo se eligió teniendo en cuenta el promedio en el número de iteraciones, considerando las veces en que el algoritmo aceptó la búsqueda del mínimo global. Se encontró que un tamaño de 20 a 30 individuos por generación es propicio para obtención de buenos resultados. Cabe aclarar que el tamaño de la población es constante en cada generación [30].

De acuerdo con las recomendaciones pertinentes para la tasa de cruce, se tuvo en cuenta que a este parámetro se le debe asignar un alta de probabilidad que permita garantizar, por lo menos, que la mitad de la nueva po- blación esté constituida a partir del cruce genético de los cromosomas de los mejores individuos de la población anterior, donde la mejor tasa de cruce fue de 0,5.

La tasa de cruce influye en el número de interacciones gastadas para la obtención del mínimo global [29]. En ese sentido, se entiende que se debe a que si se toma una tasa de cruce baja, se estaría restringiendo la creación que hereden algunas características de los padres a cambio de la conservación de individuos que nunca se adapten.

En cuanto a las recomendaciones pertinentes para la tasa de mutación, se sabe que a este parámetro se le debe asignar una baja probabilidad, que permita garan- tizar, por lo menos, un caso en el que se cree un nuevo individuo ajeno a las características que le puedan heredar los padres [29]. El rango adecuado para la tasa de mutación, de acuerdo a los resultados obtenidos en la implementación sobre funciones multivariables, es de 0,1 a 0,5.

(1) Ventajas del algoritmo GA

Es posible relacionar el funcionamiento del algoritmo genético con los procesos de cruce y mutación existentes en el proceso evolutivo que presentan las especies en la naturaleza.

Permite el ajuste directo en la característica de la búsqueda que se quiere realizar (búsqueda global o local), por medio de la asignación de valores en las tasas de cruce Tc y tasas de mutación Tm.

Las diversas formas que se presentan en la naturaleza pueden ser plasmadas en el algoritmo como, por ejemplo: la selección de los mejores individuos por torneo, eli- tismo, nivel de adaptabilidad, entre otros [31].

(2) Desventajas del algoritmo GA

La pérdida de precisión en los Datos de entrada cuando la conversión de números decimales binarios no es exacta.

La tendencia a converger prematuramente. Se evidencia que los cambios entre el mejor individuo a través de las generaciones son mínimo por el cual el algoritmo con- verge con rapidez.

Las diferentes alternativas que se pueden implementar en este proceso de selección podrían ocasionar una varia- ción en la dinámica del algoritmo GA.

c) Discusión

El incremento de la población permite una mayor infor- mación del espacio de solución y, con ello, garantiza una mejor precisión con respecto al punto encontrado.

Por otra parte, una mayor cantidad de individuos per- mite la disminución del número de interacciones, ya que no es necesario esperar varias generaciones para obtener un individuo en particular, tal y como ocurre en poblaciones pequeñas.

Es imprescindible tener en cuenta que la interpretación del algoritmo GA es muy diferente a la del PSO y, por tanto, es erróneo esperar un comportamiento en los in- dividuos generación tras generación, puesto que se trata de un enjambre que no se mueve de acuerdo al tipo de función, sino conforme a una serie de procesos de cruce y mutación, de tal manera que los nuevos individuos, a pesar de conservar las características de los padres, son nuevos puntos.

IV. CONCLUSIONES

El diseño de algoritmos para aplicarlos a un estado de optimización requiere inteligencia lógico-matemática y utilizar diferentes herramientas del programa, con el objetivo de hallar las mejores soluciones. Además, se entiende que cada algoritmo agrupa una serie de grupos para ubicarles su respectivo patrón. El algoritmo ge- nético estudia los aspectos evolutivos y el algoritmo de enjambres identifica los grupos y los sectoriza.

AGRADECIMIENTOS

Los autores agradecen las contribuciones. X. Austan, A. H. Burgmeyer, C. J. Essel y S. H. Gold para la versión original en inglés de este documento. Asimismo, agradecen a

C. Bravo y F. Crispino (Brasil), M. Cotorogea (México) y

L. Antón, M. Castro J. García y M. Luque (España), por su ayuda en el establecimiento de criterios lingüísticos y el desarrollo de ejemplos de referencia.

REFERENCIAS

[1] Complex systems and AI, “Algoritmos de enjambre”, complex-systems-ai.com, 2022. [En línea]. Disponible: https://complex-systems-ai. com/es/algoritmos-desaims/

[2] J. A. de la Vega, I. Aguilar Juárez, F. García Lamont y H. Gómez Ayala. Introducción al análisis de algoritmos. Guadalajara, México: Cenid, 2019.

[3] A. Moujahid, I. Inza y P. Larrañag, P. Tema 2. Algoritmos Genéticos. Departamento de Ciencias de la Computación e Inteligencia Artificial, Uni- versidad del País Vasco, 2018.

[4] C. E. Toca Torres, “Inteligencia colectiva: enfoque para el análisis de redes”, Est. Gerenc., vol. 30, n.º 132, pp. 259–266, jul. 2014, doi: 10.1016/j. estger.2014.01.014.

[5] AcademiaLab. ”Comportamiento de Enjambre”, academia-lab.com, 2022. [En línea]. Disponible: https://academia-lab.com/enciclopedia/ comportamiento-de-enjambre/

[6] Aguión, A. “La inteligencia de enjambre”, fundacionaquae.org, 2020. [En línea]. Disponible: https://www.fundacionaquae.org/la-inteligencia- enjambre-y-la-inteligencia-artificial/

[7] Amat, J. R. “Optimización con enjambre de partículas”,cienciadedatos.net, 2019. [En línea]. Disponible: https://www.cienciadedatos.net/doc- umentos/49_optimizacion_con_particle_swarm”,

[8] M. D. Arango Serna, L. F. Campuzano Zapata y J. A. Zapata Cortés. “Mejoramiento de procesos de manufactura utilizando Kanban”. Rev. Ing. Univ. Medellín, vol. 14, n.º 27, pp. 221-234, 2015.

[9] C. Darwin, “Capítulo IV: Selección natural, o la supervivencia de los más adecuados”, en El origen de las especies por medio de la selección natural [En línea]. Disponible en: https://www. cervantesvirtual.com/nd/ark:/59851/bmcd21v0,

[10] Blog Profesores Elo.”Control de congestión”, profesores.elo.utfsm.cl, 2018. [En línea]. Dispo- nible: http://profesores.elo.utfsm.cl/~agv/elo322 /1s02/lectures/congestion.pdf

[11] F. Charles, F. Velázquez Dodge y M. Mejía Lavalle. Análisis del algoritmo de optimización de en- jambres de partículas utilizando una aplicación de gráficos 3D. Morelos, Mexico: Centro Nacional de Investigación y Desarrollo Tecnológico Cuernavaca, 2016.

[12] Cloudflare. “Que es el enrutamiento? Enrutamiento IP”, cloudflare.com,2022. [En línea]. Disponible: https://www.cloudflare.com/es-es/learning/net- work-layer/what-is-routing/#:~:text=El%20enruta- miento%20de%20redes%20es,telef%C3%B3nicas%20 hasta%20el%20transporte%20p%C3%BAblico.

[13] Conogasi. “Algoritmos Geneticos”, conogasi.org, 2018, [En línea]. Disponible: https://conogasi.org/ articulos/algoritmos-geneticos/

[14] Correduría Inteligente. “La seguridad en las comunicaciones”, mpmsoftware.com, 2019. [En línea]. Disponible: https://www.mpmsoftware. com/es/blog/seguridad-en-las-comunicaciones/

[15] G. Crespo Sánchez, I. Pérez Abril y Z. García Sánchez. Investigación científica sobre algoritmos evolutivos para la reconfiguración óptima de redes de distribución de energía., Santa Clara, Cuba: Universidad y Sociedad 2022.

[16] N. A. Domínguez. Navegando por las inmensidades culturales.Buenos Aires, Argentina: Instituto de Publicaciones Navales, 2020.

[17] J. M. Fernández Orchando. Cada punto en el espacio de búsqueda tiene asociado un valor numérico denominado valor de adaptación. Madrid, España: Universidad Politécnica de Madrid, 2018.

[18] Khan Academy. “Darwin, evolución y selección natural”, es.khanacademy.org/science, 2020. [En línea]. Disponible: https://es.khanacademy.org/ science/ap-biology/natural-selection/natural- selection-ap/a/darwin-evolution-natural-selection

[19] Lorbes, M. “Metodología basada en algoritmos genéticos y optimización de enjambres de par- tículas para determinar la matriz de peso del modificador lineal cuadrado”, Univ. Cienc. Tecnol., vol. 23, n.º 95, pp. 95-102, dic. 2019, .

[20] Mathworks. “Global Optimization Toolbox” la.mathworks.com. 2022. [En línea]. Disponible: https://la.mathworks.com/products/global- optimization.html

[21] Nieto Fuentes, R. Optimización con componentes interdependientes. Centro de Investigación en Matemáticas, Guanajuato, 2018.

[22] J. M. Ochotorena Ferreras, B. A. Sabrido y G. L. Armero. Genética y evolucion darwianiana, Espasa, Madrid, 2020, pág 36.

[23] G. D. Rodríguez Acevedo. “Ciencia, Tecnología y Sociedad: Una mirada desde la Educación en Tecnología”, Rev. Iberoam. Educ., n.º 18. [En línea]. Disponible en: https://rieoei.org/historico/ oeivirt/rie18a05.htm.

[24] R. Eberhart y J. Kennedy, James. “A new optimizer using particle swarm theory”, en Proceedings of the Sixth International Symposium on Micro Machine and Human Science, 1995, pp. 39-43.

[25] Y. Shi y R. Eberhart. “A modified particle swarm optimizer”, en 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence (Cat. No. 98TH8360), pp. 69-73.

[26] C. Arias y R. Aguilar. “Soluciones de sistemas de ecuaciones no lineales mediante el método metaheurístico PSO”. Trabajo de grado, Fac. de Ing. Fís.-Mec., Univ. Ind. de Santander. Bucaramanga, Colombia, 2011.

[27] K. Barragán y D. Vanegas. “Real potencial del uso del método de análisis de intervalos para la optimización con restricciones frente al PSO de convergencia garantizada”. Trabajo de grado, Fac. de Ing. Fís.-Mec., Univ. Ind. de Santander. Bucaramanga, Colombia, 2010.

[28] J. Plata y S. Reyes. “Determinación de raíces reales y complejas en sistemas de ecuaciones utilizando optimización por enjambre de partículas (PSO)”. Trabajo de grado, Fac. de Ing. Fís.-Mec., Univ. Ind. de Santander. Bucaramanga, Colombia, 2011.

[29] P. Stoffa y S. Mrinal. Global Optimization Methods in Geophysical Inversión. Amsterdam, Netherlands: Elsevier Science, 1995.

[30] J. Molina y E. Páez. “Optimización del peso de cerchas en 3D mediante Algoritmos Genéticos (GA) y optimización por Enjambre de Partículas (PSO)”. Trabajo de grado, Fac. de Ing. Físico-Mecánicas. Univ. Ind. de Santander. Bucaramanga, Colombia, 2010.

[31] J. Cruz. “Ejemplo de algoritmo genético en Matlab código y funciones”. cienciafisicamatlab.blogspot. com. http://cienciafisicamatlab.blogspot.com/ 2011/11/ejemplo-de-algoritmo-genetico-en- matlab.html (Consultado: 30 de junio, 2014).