I. INTRODUCCIÓN

Las metodologías de planificación de cultivos revisadas han permitido verificar que varios métodos de pronóstico pretenden estimar volúmenes de producción en especies de frutales. Los modelos utilizados con frecuencia son simulación [1], estadísticos-ambientales y estadísticos- biométricos, y estadísticos por muestreo [2]. El fundamento científico-técnico de los pronósticos de producción se basa en el conocimiento de la fisiología, la fenología y los factores meteorológicos, y cuenta con el apoyo de la estadística [2], para que cumplan con exactitud la predicción y sean de utilidad para otros especialistas [3], [4] y [5]. Para el objetivo de esta investigación se aplicaron los métodos de Regresión Múltiple y Modelo Autorregresivo Integrado de Promedio Móvil (ARIMA, por sus siglas en inglés) ampliamente reportados y recomendados en la literatura para estimar el rendimiento a partir de variables agroclimáticas, analizar su ajuste y ventajas de su aplicación a través del caso seleccionado [2], [6] y [7]. Los pronósticos pretenden capturar de manera más cercana la dinámica de cada una de las prácticas culturales (transitorias y permanentes), teniendo en cuenta el ciclo de producción [8].

La regresión recoge la correspondencia entre las variables calculadas y distintas variables independientes. Los residuos representan la variabilidad que no queda recogida por la relación determinista representada por las funciones de regresión [9], [10].

En el modelo de regresión lineal múltiple la variable dependiente o de respuesta “Y” está relacionada con más de una variable de explicación [11].

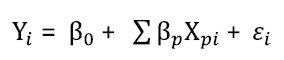[Ecuación 1]

Donde las perturbaciones son el error asociado a la medición i del valor de , bajo los supuestos de que . El análisis entre dos o más variables se puede realizar a través de ecuaciones, como se propone con este método de análisis estadístico.

Por otro lado, ARIMA es una metodología propuesta por Box y Jenkins (1976)[16] que ha sido ampliamente utilizada en todos los ámbitos científico-técnicos para identificar procesos estocásticos temporales y estimar modelos para su predicción y control. En el modelo ARIMA (p, d, q), p se define como el orden del proceso autorregresivo; d es el número de diferencias que son necesarias para que un proceso sea estacionario, y q es el orden del proceso de medias móviles se puede representar como:

[Ecuación 2]

En la ecuación 2, d corresponde a las diferencias d, que sirven para convertir la serie original en estacionaria. Los parámetros ,…., son la parte autorregresiva; ,…, pertenece a las media móviles, al término constante y a la perturbación estocástica. Esta metodología se basa en la utilización de los datos de una variable para identificar las características de su estructura probabilística subyacente, en contraposición a los procedimientos tradicionales de identificación de modelos basados en una teoría explicativa del fenómeno en estudio [12].

La producción de especies pasifloras como el maracuyá depende de variables agroclimáticas, por ejemplo, altitud, temperatura, humedad relativa, radiación, precipitación, velocidad del viento, brillo solar, entre otras. Estas son variables externas cuyas condiciones no se pueden controlar y afectan de manera directa el rendimiento del cultivo, lo que se convierte en una limitante para la toma de decisiones por parte del agricultor en cuanto a la planificación del cultivo, ya que su conocimiento es intuitivo (cultural o aprendido) frente al comportamiento del clima y su incidencia con el cultivo [13]. De esta manera los agricultores enfrentan la incertidumbre con consecuencias económicas de sus acciones, por su limitada capacidad para predecir el clima, los precios y las respuestas biológicas debido a las diferentes prácticas agrícolas. Por esta razón, es definitivo el análisis de la incertidumbre y el riesgo, a través de técnicas cuantitativas para minimizar las pérdidas económicas [14]. Así, el objetivo de esta investigación es diseñar modelos de apoyo para las decisiones en planificación de cultivos, que permitan entender el comportamiento de la dinámica en los sistemas complejos, como son los agroecosistemas, para proponer criterios de respuesta, y de esta manera mitigar el impacto de la incertidumbre y del riesgo por efecto del clima en la producción de los cultivos, que afecta la disponibilidad y el abastecimiento en el mercado [15].

II. METODOLOGÍA

Para lograr el objetivo propuesto se realizó un análisis descriptivo exploratorio, calculando las medidas de estadística descriptiva clásica y así elaborar los modelos de pronóstico. Se hizo un análisis de regresión múltiple para explorar la relación entre el rendimiento de maracuyá en el municipio de La plata, Huila, Colombia, situado en la cordillera Central 2º23’00’’ de latitud Norte 75º56’00’’ y de longitud Oeste, con una temperatura media de 23º C y una altitud de 118 m s. n. m, en función del conjunto de variables agroclimáticas: temperatura, brillo solar, humedad relativa y precipitación. Para esto se utilizó un proceso de regresión paso a paso backwards¹, que permite identificar el mejor modelo de regresión lineal múltiple para elaborar el pronóstico. Para el modelo ARIMA se realizó análisis de la serie de tiempo para la variable de rendimiento, identificando el mejor modelo para hacer el pronóstico.

En la Figura 1 se describen los pasos para establecer el pronóstico de rendimiento del cultivo de maracuyá a través de su relación con las variables agroclimáticas.

Figura 1.
Metodología de investigación
Fuente: elaboración propia.

La recolección de los datos históricos promedio mensuales de las variables agroclimáticas, altitud, temperatura, humedad relativa, radiación y precipitación se llevó a cabo desde 2007 hasta 2014, a través de lecturas tomadas de la estación climatológica con código 21055020 y nombre Esc Agr La plata, ubicada en la latitud 2,3782 y longitud -75,89125 en el municipio de La Plata, perteneciente al Instituto de Hidrología, Meteorología y Estudios Ambientales (IDEAM), y de los rendimientos en kilogramos mensuales del cultivo de maracuyá en La Plata (ver figura 1), tomados por el Ministerio de Agricultura y Desarrollo Rural de Colombia. Para la selección de los datos se estableció un nivel de completitud de 75 % o más para acceder a la construcción de un modelo más robusto y procurar una mínima falta de información.

III. RESULTADOS

A. Análisis descriptivo exploratorio

Con los datos recolectados se realizó el análisis descriptivo exploratorio, que incluyó el cálculo de medidas descriptivas clásicas, para elaborar las matrices de dispersión, las cuales permitieron observar las relaciones entre el rendimiento de maracuyá y las variables agroclimáticas; la matriz de correlación de variables para rendimiento en toneladas de maracuyá y para las variables agroclimáticas asociadas al mismo mes de observación. Los análisis fueron efectuados utilizando la versión 3.4.4 del Lenguaje R (lenguaje de programación para procesamiento estadístico y elaboración de gráficos) (R Core Team, 2018), usando la versión 1.1.442 de RStudio (disponible en https://www. rstudio.com/).

Los análisis estadísticos exploratorios se hicieron teniendo en cuenta los libros de metodología estadística [16], [17], [18] y [19] y gracias a estos se obtuvo lo siguiente para cada variable (Tabla 1).

Tabla 1

Valores estadísticos descriptivos

Fuente: elaboración propia.

En términos generales, las medidas estadísticas de tendencia central presentadas en la Tabla 1 sugieren una distribución normal del comportamiento de las variables agroclimáticas.

El rendimiento promedio de maracuyá fue de 206,6 kg*ha-1 para los siete años considerados; el 75 % de esta variable alcanzó como valor máximo 247,8 kg*ha-1, con un valor máximo total de 368,5 kg*ha-1. En la Figura 2 se presenta la distribución normal de esta variable. En el caso de las variables agroclimáticas, la precipitación tiene una alta variabilidad, pues sus registros oscilan entre 10 mm/mes hasta los 364,7 mm/mes; un caso similar se encontró para el brillo solar, que va desde 54,2 horas/mes hasta 218,9 horas/mes promedio. La humedad no supera el 87 %.

Figura 2.
Histograma de rendimiento del maracuyá
Fuente: elaboración propia.

En la Figura 3 se observa el patrón cíclico de variación anual, y se puede notar un mayor rendimiento en febrero y marzo, y uno menor entre julio y agosto. Se encuentra además una variabilidad similar en el rendimiento para los distintos meses del año, sin la presencia de valores extremos.

Figura 3.
Cajas múltiples del rendimiento de maracuyá por meses
Fuente: elaboración propia.

En la Figura 4 se presentan los diagramas de cajas para las variables agroclimáticas, que muestran marcadas variaciones cíclicas anuales en relación con la variable rendimiento. Estas variables fueron humedad y precipitación. Se encontraron variaciones cíclicas anuales menos marcadas para la variable temperatura y algunos valores atípicos en algunos meses en los datos de las variables brillo solar y precipitación.

Figura 4.
Cajas para las variables agroclimáticas temperatura y humedad
Fuente: elaboración propia.

Continuando con la matriz de dispersión de las variables en estudio, esta se encuentra sustentada en la matriz de correlaciones bivariadas de la Tabla 2.

Tabla 2.

Matriz de correlación cruzada entre variables

Fuente: elaboración propia.

La matriz de correlaciones bivariadas muestra una asociación no lineal directa entre la humedad y 1 precipitación (0,630); las demás variables presentas coeficientes de aproximadamente 0,349, que son menos fuertes y no permiten determinar asociaciones lineales directas.

B. Modelo de regresión lineal múltiple para explicar y predecir la variable rendimiento

Partiendo del anterior análisis estadístico descriptivo, se plantea el modelo de todas las variables agroclimáticas aplicando la metodología backward de eliminación de variables menos significativas, [18]. Para esta metodología se probaron cinco modelos hasta encontrar las variables agroclimáticas que mejor explicaban el rendimiento de maracuyá.

Debido a que el análisis estadístico no mostró una asociación lineal fuerte entre variables, se determinó el modelo regresión múltiple para explicar el rendimiento, no se puede aplicar para pronosticar el rendimiento del maracuyá. Por esto se debe utilizar únicamente el modelo basado en la humedad, cuya correlación se acerca al valor 0,7, que resulta significativo al 5 % (ver Tabla 3).

Tabla 3.

Coeficientes estimados del modelo final

Se observa que hay un p-valor que es significativamente menor a 0,05 (0,0103) en humedad. Adicionalmente, se tiene que el valor de probabilidad del estadístico F indica que el modelo es significativo al 5 %, al ser su p-valor (0,000828) menor que 0,05. Se reconoce también una baja variabilidad del rendimiento explicada a través del modelo, evidenciado a través del R cuadrado (0,1856) y del R cuadrado ajustado (0,1498) [20].

A pesar de que el ajuste del modelo es tan bajo y que sugiere la posibilidad de estimación de un modelo descriptivo, para efectos prácticos de la investigación se decide continuar con el análisis de residuos (Figura 5), como validación de los supuestos que dan el soporte esta- dístico a las estimaciones y predicciones del modelo.

Figura 5.
a y b. Gráfico análisis de residuos
Fuente: elaboración propia.

El análisis de residuos (Figura 5a) muestra los residuos y los residuos estudentizados contra los valores ajustados del modelo, en los que no se observa algún patrón particular de los puntos; esto evidencia clara del cumplimiento del supuesto de homocedasticidad (igualdad de varianza). En la Figura 5b se muestra el gráfico de probabilidad normal, con una línea recta de los residuos estudentizados, que asegura la normalidad de los errores y no se observan valores atípicos.

Se constató que existen correlaciones bajas entre las variables explicativas del modelo propuesto, razón por la cual se valida el supuesto de no multicolinealidad entre las variables regresoras.

El modelo de regresión lineal múltiple estimada toma la siguiente expresión:

Ecuación 3. Rendimiento = -319,2503 + 4,5814 *(Humedad)

Con esta expresión se puede afirmar que por cada unidad que incrementa la humedad, el rendimiento aumenta en 4,58 kilogramos.

En términos generales, es importante acotar que el ajuste del modelo es muy bajo (R=0,1856), lo que señala que dicho modelo es descriptivo y no predictivo, y que depende de la variable humedad. Por esto pierde su objetivo principal de ser múltiple, aunque para efectos comparativos se harán los pronósticos usando este modelo. Esta situación se debe a que en este caso las variables agroclimáticas por sí solas no definen completamente el rendimiento en kilogramos de maracuyá por ha y en su defecto se propone considerar otras variables como fertilizantes, suelos, etc.

C. Modelo ARIMA de series de tiempo para predecir la variable rendimiento

Los modelos ARIMA se obtienen siguiendo la metodología de Box y Jenkins [16]. Es importante acotar que dentro de la selección del mejor modelo para predecir la serie estudiada, se usó el criterio de información de Akaike (AIC) [20], para el cual a menores valores de estas medidas mejor modelo en términos de la calidad relativa, con relación a la pérdida de información del modelo estadístico estimado para la serie de rendimiento del cultivo.

El primer paso es la creación de los datos en una estructura de series de tiempo en R [11], [12], [17] y [21]. Seguido de esto, se procede a hacer el análisis correspondiente; después se evalúa la estacionariedad, estacionalidad y descomposición de la serie, como se observa en la Figura 6, de la variable rendimiento en el horizonte de tiempo analizada.

Figura 6.
Serie de tiempo del rendimiento del maracuyá
Fuente: elaboración propia.

La serie original (Figura 6) permite ver un patrón cíclico de periodicidad anual con picos superiores en el primer trimestre del año y picos inferiores en tercer trimestre del año, con una ligera tendencia a partir de 2011, que se mantiene hasta 2014, cuando el máximo rendimiento de la serie supera las 250 toneladas de maracuyá.

Con la metodología establecida se realizó la descomposición de la serie en su parte estacional, de tendencia y cíclica. La Figura 7 muestra un patrón cíclico anual que disminuye en sus valores más altos a lo largo del tiempo y una tendencia variable a través de los años; es decir, entre 2007 y 2008 la tendencia es creciente, y sus valores se mantienen contantes por lo menos hasta 2011, cuando la tendencia es al decrecimiento continuo y acelerado hasta 2013, año en que la serie retoma la tendencia creciente, menos pronunciada que en años anteriores.

Figura 7.
Descomposición de la serie de tiempo del rendimiento del Maracuyá
Fuente: elaboración propia.

En el Figura se observa además que la serie pareciera ser estacionaria, resultado que se corrobora con la prueba de Dickey y Fuller, así:

Estadístico Dickey-Fuller = - 4,2586 Lag order = 4 P-Value = 0.01

Con estos valores la hipótesis por probar es que la serie no es estacionaria, con lo cual al 5 % de significación se rechaza la hipótesis, lo que deja claro la estacionariedad de la serie.

Los autocorrelogramas simple (ACF) y parcial (parcial ACF) de la Figura 8 comprueban que el patrón es cíclico, ya que en el gráfico de autocorrelación parcial se evidencia la correlación de un periodo de ciclo anual; por lo tanto, en búsqueda del mejor modelo ajustado a la serie, se usa la función auto.arima de la librería forecast [22], donde se puede ver que el mejor modelo ARIMA es el ARIMA (0, 1, 0).

Figura 8.
Autocorrelaciones simple y parcial
Fuente: elaboración propia.

Con ARIMA (0,1,0) Con Estimated as 199,3 Log likelihood = - 386,31 AIC = 774,63 AICc = 774,67 BIC = 777,1

Al obtener el gráfico de residuos del modelo 1 propuesto, se reconoce la necesidad de corregir la serie, tomando un p o q igual a 12; así, en un segundo modelo propuesto se toma q = 12 (modelo de promedios móviles), y se obtiene un modelo estimado:

[Ecuación 4]

La Figura 9 de residuos muestra cómo se corrigen las distorsiones del modelo original, pero su capacidad predictiva es menor por tener un AIC mayor que en el primero.

Figura 9.
Residuos para el modelo 2 ARIMA (0, 1, 12)
Fuente: elaboración propia.

De este último modelo, una segunda elección es considerar un modelo autorregresivo de orden 12, con el cual se obtiene la siguiente ecuación del modelo:

[Ecuación 5]

El gráfico de residuos del tercer modelo (Figura 10) corrige las posibles distorsiones del modelo original, y el AIC es ligeramente superior a este, pero menor al segundo modelo; por esta razón, se clasificaría ese modelo como el mejor.

Figura 10.
Residuos para el modelo 3 ARIMA (12, 1, 0)
Fuente: elaboración propia.

Teniendo en cuenta el ajuste de los 3 modelos propuestos y la decisión tomada anteriormente, el pronóstico para el primer semestre de 2015 se propone en la Tabla 4. Los pronósticos del modelo y sus límites de confianza al 95 % muestran en términos general que la serie no presenta variaciones en el siguiente semestre a los valores observados, pero con valores superiores a diciembre de 2014.

Tabla 4.

Pronóstico de rendimiento del maracuyá con el modelo ARIMA (12, 1, 0)

D. Comparando el modelo de regresión lineal múltiple y ARIMA

Los modelos de regresión lineal múltiple y ARIMA no son comparables, debido a que son ajustados por metodologías completamente diferentes, pero ambos se pueden usar con fines predictivos, como se propone en la literatura. Los primeros exponen el rendimiento a través de algunas variables explicativas y los segundos por medio de la historia de la serie a través de sus componentes autorregresivos, de promedios móviles y de la suavización de la tendencia.

Sin embargo, dados los resultados anteriores y el bajo ajuste de los modelos de pronóstico, se recomienda su utilización con fines descriptivos.

En el mismo se puede observar que en los años iniciales, el modelo tiende a subestimar los picos de mayor rendimiento, ya que no es capaz de tomar en cuenta las variaciones temporales, que es una de las ventajas que tendría el modelo ARIMA sobre el de regresión lineal múltiple (ver Figura 11).

Figura 11.
Serie original y pronóstico de rendimiento del maracuyá con regresión lineal múltiple
Fuente: elaboración propia.

IV. DISCUSIÓN

En algunos estudios relacionados con el análisis de producción de caña de azúcar en México, con la aplicación del modelo ARIMA (1, 2, 0), el pronóstico de la producción para 2006-2007 para el ingenio, Independencia de Martínez de la Torre, fue de 11.974.06 mg de azúcar y la producción real de la zafra de referencia 2006-2007 fue de 12.736 mg (Servicio de Información Agroalimentaria y Pesquera [Siapsagarpa], 2010). El presente modelo fue diferente, en cuanto a los parámetros, al modelo ARIMA (2, 1, 2) utilizado en Pakistán, el cual analizó los datos de producción entre 1947 y 2002. De ese análisis se obtuvieron pronósticos aproximados a los reales, como ocurrió en este estudio, lo que permite concluir que el tipo de modelos mencionados pueden brindar un apoyo a la decisión, que disminuye la incertidumbre del conocimiento del rendimiento en función de las variables no controlables como las agroclimáticas.

VI. CONCLUSIONES

Se deben verificar qué condiciones climáticas afectan directamente la ecofisiología del cultivo y cosecha, ya que mediante el control de estas variables se pueden mantener las condiciones para que el fenómeno histórico se reproduzca a futuro. Algunas alternativas que pudieran considerarse más adelante son: modelos ARIMA con la inclusión de variables explicativas, modelos de regresión lineal múltiples con datos rezagados y el modelamiento de series múltiples, incluyendo en este caso a otras series correspondientes a algunas variables agroclimáticas (caudales, evaporación, etc.).

Por otro lado, en la mayoría de los métodos de análisis de datos se encontraron relaciones entre los eventos climáticos y el rendimiento del cultivo, especialmente con la distribución de la precipitación y los fenómenos que afectan la floración y el transporte de polen (velocidad del viento y porcentaje de humedad relativa) los cuales inciden en el desarrollo de la planta.

En próximas investigaciones se sugiere estimar modelos específicos y elaborar todas las pruebas de errores y coeficientes necesarias para cada variable, y así establecer que en dichos modelos exista un mayor coeficiente de ajuste, que mejoren su estabilidad y proporcionen una base válida sobre la cual se puede pronosticar resultados, para que estos se consideren aceptables y cercanos a la realidad futura.

REFERENCIAS

[1] A. M. Soto Garcés, J. M. Cortés Torres y D. Rodríguez Caicedo, “Modelo de simulación del crecimiento y desarrollo de la papa criolla Growth and development simulation model of potato”, Ciencia en Desarrollo, vol. 9, no. 1, pp. 9-20, Ene.-Jun. 2018.

[2] N. Kantanantha, “Crop decision planning under yield and price uncertainties”, Ph.D. tesis, H. Milton Stewart Sch. of Ind. and Sys. Eng. Georgia Inst. of Tech., Georgia, Estados Unidos, 2007.

[3] O. Delgadillo-Ruiz, P. P. Ramírez-Moreno, J. A. Leos-Rodríguez, J. M. Salas González y R. D. Valdez-Cepeda, “Pronósticos y series de tiempo de rendimientos de granos básicos en México”, Acta Univ., Vol. 26, No. 3, pp. 23-32, 2016.

[4] J. Ruiz-Ramírez, G. E. Hernández Rodríguez y R. Zuleta-Rodríguez, “Análisis de series de tiempo en el pronóstico de la producción de caña de azúcar”, Terra Latin. Vol. 29, No. 1. 2011 [En línea]. Disponible en: http://www.scielo.org.mx/scielo.php?script=sci_ arttext&pid=S0187-57792011000100103.

[5] C. Martínez Ventura, “Pronósticos de producción agrícola”, Archivos de Eco., abr. 2006.

[6] R. D. Kusumastuti, D. P. Van Donk, and R. Teunter, “Crop-related harvesting and processing planning: A review”, Int. J. Prod. Econ., Vol. 174, pp. 76-92, 2016.

[7] O. Musshoff and N. Hirschauer, “What benefits are to be derived from improved farm program planning approaches? – The role of time series models and stochastic optimization”, Agric. Syst., Vol. 95, No. 1-3, pp. 11-27, Dic. 2007.

[8] C. Martínez Ventura, “Pronósticos de producción agrícola”, Departamento Nacional de Planeación; DNP, 2006.

[9] T. H. Hengl, A Practical Guide to Geostatistical Mapping. Luxemburgo: Office for Official Publications of the European Communities, 2009.

[10] T. Hengl, G. B. M. Heuvelink, and D. G. Rossiter, “About regression-kriging: From equations to case studies”, Comput. Geosci., Vol. 33, No. 10, pp. 1301-1315, Oct. 2007.

[11] D. Derryberry, Basic data analysis for time series with R, John Wiley & Sons, 2014.

[12] R. Dalinina, “Introduction to Forecasting with ARIMA in R” [En línea]. Disponible en: https://www. datascience.com/blog/introduction-to-forecasting- with-arima-in-r-learn-data-science-tutorials.

[13] D. Jackson., N.E. Looney, and M. Morley-Bunker, Temperate and subtropical fruit production, Inglaterra, CABI, 2011.

[14] D. J. Pannell, B. Malcolm, and R. S. Kingwell, “Are we risking too much? Perspectives on risk in farm modelling”, Agric. Econ., Vol. 23, No. 1, pp. 69-78, 2000.

[15] G. Moschini and D. A. Hennessy, “Uncertainty, risk aversion, and risk management for agricultural producers”, Handbook of Agri. Econ., Vol. 1, pp. 88- 153 2001.

[16] G. E. P. Box, G. M. Jenkins, G. C. Reinsel, and G. C. Ljung, Time Series Analysis: Forecasting and Control, 5.a ed. Nueva York, NY: John Wiley & Sons, 2015.

[17] A. V. Metcalfe and P. S. P. Cowpertwait, Introductory Time Series with R. Nueva York, NY: Springer New York, 2009.

[18] D. Montgomery, Vining, G. G. y E. A. Peck, Intro- ducción al análisis de regresión lineal, México: Limusa Wiley, 2006.

[19] R. Shumway and D. S. Stoffer, Time series regression and exploratory data analysis, Springer,2006.

[20] J. D. Cryer and K.-S. Chan, Time Series Analysis. Nueva York, NY: Springer New York, 2008.

[21] “R: The R Project for Statistical Computing” [En línea]. Disponible en: https://www.r-project.org/.

[22] R. J. Hyndman and Y. Khandakar, “Automatic Time Series Forecasting: The forecast Package for R”, J. Stat. Softw., Vol. 27, No. 3, 2008.

Notas