
Omaira Elizabeth González-Giraldo
Omaira.gonzalez@unillanos.edu.co
Universidad de los Llanos Villavicencio –Colombia
María Teresa Castellanos Sánchez
mcastellanos@unillanos.edu.co
Universidad de los Llanos Villavicencio-Colombia
Encuentre este artículo en: http://revistas.uniminuto.edu/index.php/IYD
Fecha
de recepción: 6 de enero de 2019
Fecha de aceptación: 12 de abril de 2019
Fecha de publicación: 30 de junio de 2019
El artículo muestra los resultados logrados durante el 2015 en la Institución Educativa Alberto Lleras Camargo del Departamento del Meta, Colombia. El propósito de esta investigación es establecer las relaciones entre las variables ábaco cerrado y los procesos de aprendizaje aritméticos de la multiplicación y la división de 120 niños de tercer grado de básica primaria con y sin limitación visual. La propuesta pedagógica implementa las situaciones de la enseñanza con el ábaco cerrado: Situaciones de acción, formulación, validación y de institucionalización. Como resultados de la investigación se encuentran dos hechos, el primero que los procesos de enseñanza y aprendizaje del conocimiento matemático con el ábaco cerrado disminuyen la ruptura pedagógica en la escuela y el segundo, el fortaleciendo de currículos inclusivos permite una educación básica primaria para todos los infantes.
Palabras clave: ábaco, ábaco cerrado, operaciones aritméticas, situaciones didácticas, instituciones educativas públicas.
ABSTRACT
The article shows the results achieved during 2015 at the Alberto Lleras Camargo Educational Institution in Meta, Colombia. The purpose of this research is to establish the relationship between closed abacus variables and arithmetic learning process immerse in the multiplication and division operation with 120 children of third grade primary school, with and without visual limitations. The pedagogical proposal implements the situation of teaching with the closed abacus: Situations of action, formulation, validation and institutionalization. As a research results,two facts were found, the first is that the processes of teaching and learning of mathematical knowledge with the closed abacus decrease the pedagogical rupture in school and the second, strengthening of inclusive curricula allows a primary basic education for all infants.
Keywords: abacus, closed abacus, arithmetic operations, didactic situation, public educational institutions.
La enseñanza de las matemáticas constituye una preocupación social generalizada para proporcionar a los niños- niñas y jóvenes herramientas cognitivas y simbólicas que les permitan aprender las operaciones de la aritmética. Una forma visible de esta problemática radica en la apatía hacia el área de las matemáticas mostrada por los estudiantes en los grados de básica primaria, evidenciados en resistencia al desarrollo de actividades escolares; la continua búsqueda de excusas para no asistir o poca participación en la clase de matemáticas.
Esta situación de algunos estudiantes de apatía hacia las matemáticas, se incrementa por el modelo pedagógico que subyace a la enseñanza de las matemáticas desde la repetición oral/ escrita que es descontextualizada de la cotidianidad de los/ las estudiantes, con la enseñanza de los algoritmos de adición, sustracción y multiplicación efectuándose mecánicamente desde la oralidad, con ejercicios modelo repetidos por los estudiantes, desde lo simbólico axiomático, sin atender a las características de pensamiento de los estudiantes. Andrade (2011) señala:
Los errores más frecuentes, en niños de 7 a 12 años, se presentan en el sistema de numeración decimal y en los números racionales sin signo. Por ejemplo, […] se presentan los siguientes errores, entre muchos otros casos: dar el valor de la cifra de acuerdo a su posición en el número; sumar números cuando la suma de las unidades es mayor que la decena; restar números cuando las unidades que se restan son mayores; dar el paso de la suma a la multiplicación; […]. P. 3
Así, el aprendizaje de las matemáticas en la básica primaria encuentra dificultades en relación con las nociones de número: ordinalidad, cardinalidad, y conteo, el profesor espera un proceso madurativo de los niños que les permita superar esta situación, desconociendo la importancia de estas primeras nociones para la construcción del número y la comprensión de las operaciones de adición y sustracción en segundo grado y multiplicación y división en el tercer grado de la básica primaria. Se desconocen por parte de los profesores para la enseñanza y el aprendizaje de la matemática los elementos del desarrollo histórico, conceptual y estructural de la disciplina y la didáctica.
En las instituciones escolares cuyo proyecto educativo es inclusivo (atiende poblaciones con limitaciones o excepcionalidad), la enseñanza de las matemáticas en los grados iniciales obedece a diferentes modelos pedagógicos que incluye el ábaco como soporte didáctico. Abordar el estudio del pensamiento aritmético desde las posibilidades que el permite el ábaco cerrado como mediación pedagógica permitirá estimar las condiciones y dinámicas pertinentes en la enseñanza de la multiplicación y división como un proceso constructivo por los niños.
Figura 1. Cartilla INCI (2000). Ábaco cerrado

El ábaco Japonés (ábaco cerrado) está formado por un bastidor rectangular con una serie de bolas denominadas cuentas que se deslizan a lo largo de unas varillas o ejes, un ábaco puede contar con 13, 21 y 27 ejes; una barra horizontal divide el instrumento en dos partes, la superior comprende una hilera de cuentas con valor igual a 5 y en la parte inferior 4 hileras de cuentas de un valor igual a 1, en la barra horizontal aparece cada 3 varillas un punto en alto relieve que representa el punto de mil, millón, la coma decimal entre otros, para un total de 6 puntos que se enumeran de derecha a izquierda.
Los puntos dividen el ábaco en siete clases: La primera clase va del marco del lado derecho hasta donde se encuentra el primer punto que corresponde a las centenas, la segunda clase se encuentra entre el primer y segundo punto que corresponde a los miles, la tercera clase esta entre el segundo y tercer punto que corresponde a los millones, y así sucesivamente hasta la séptima clase, que está entre el sexto punto y el marco del lado izquierdo del ábaco. En el ábaco se escriben los números de izquierda a derecha, las cantidades se pueden escribir al lado derecho, en la mitad o a la izquierda preferiblemente se hace a la derecha en el caso que las cantidades tengan ceros para que no se preste a confusión. El valor de las cuentas está determinado por su posición y solo adquiere su valor cuando se les empuja hacia la barra horizontal. (Instituto nacional para ciegos INCI. Cartilla Abaco Primera parte. 2000, p. 7)
El ábaco cerrado (sorobá) es un instrumento de acción-reflexión que reúne cualidades de primer orden para el aprendizaje de las ideas esenciales del concepto de sistema posicional de numeración. Madrid, P. y Rosa, A. (2003) consideran que:
El ábaco es una herramienta que permite jugar, profundizar en los conceptos de clasificación y ordenación, desarrollar la inventiva y el gusto por formas variadas y simétricas, iniciar en la búsqueda de posibilidades combinatorias, como el medio para alejarse de una aritmética basada en una colección de símbolos escritos números y de expresiones con dichos números que hay que aprender de un modo formal. Al basarse en contextos materiales suficientemente atractivos, el ábaco provoca la actividad mental del alumno. Porque las matemáticas…tratan de ideas que cada alumno debe construir en su mente y que son consecuencia de experiencias y acciones
El aprendizaje desde los procesos de sensación y percepción que el uso del ábaco cerrado facilita como un primer momento, permite por parte del estudiante una posterior construcción y representación en lo figurativo y simbólico del número y la operacionalización con estos, atiende a las características de desarrollo de pensamiento y conocimiento por parte del sujeto desde una abstracción empírica a una abstracción reflexiva. El aprendizaje de las matemáticas desde los niveles iníciales de básica se facilita cuando el estudiante ha realizado una comprensión y construcción de las nociones básicas de número (ordinalidad y cardinalidad) y de las relaciones entre éstos; esto permite el aprendizaje del número y de las operaciones en el uso en situaciones cotidianas, en problemas formulados y la generalización de los conceptos; la construcción de las operaciones de adición y sustracción y la resolución de problemas.
En el mismo sentido DAmore y Fandiño (2015)
Aunque el ábaco es un instrumento simple y atractivo, es necesario repensar su función didáctica; un objeto histórico, colocado en el tiempo, interesante, pero ciertamente no una panacea. Se puede utilizar básicamente para mostrar el significado del valor posicional de las cifras que expresan números naturales. Pero debe ser un objeto concreto, posible de tocar y manipular, no sólo un diseño en el tablero o en el libro de texto. Cada columna debe contener nueve bolitas, o fichas; porque, en el momento de agregar la décima, las nueve ya colocadas y la décima de agregar se deben quitar y sólo una de ellas debe colocarse en la columna inmediata a la izquierda. Este es el sentido del sistema de base diez (p. 28)
El ábaco cerrado facilita la resolución de problemas de adicción, sustracción, multiplicación, división y aprendizaje de los fraccionarios en tanto el niño-niña puede retirar o agregar cuentas según la operación a realizar, estableciendo un proceso desde los objetos a adicionar, sustraer, multiplicar y dividir y la representación de este ejercicio en lo figurativo- simbólico. Mediación pedagógica que atiende las características de desarrollo de pensamiento de los estudiantes de básica en donde es a partir de la manipulación de las cuentas como representación concreta de los símbolos numéricos que se apropian significativamente dichas operaciones. El ábaco permite al estudiante la interacción con las cuentas, propicia el juego, estableciendo relaciones entre los objetos de comparación, descripción, correspondencia; entre otras.
El ábaco cerrado se articula con el concepto de mediación pedagógica en tanto el maestro como creador de estrategias usa éste en la relación maestro-conocimiento- alumno. El ábaco cerrado como mediación pedagógica, permite en los espacios escolares equidad en la enseñanza de la matemática a los estudiantes y la inclusión escolar en los niveles de básica primaria, ya que los educandos con limitación visual incluidos en la escuela acceden de una forma comprensiva al conocimiento matemático, permitiendo la construcción de las operaciones básicas iníciales (adición, sustracción, multiplicación y división) y la noción de numero de una manera concreta ya que la manipulación a través del tacto como forma prioritaria en la adquisición de la información permite el desarrollo de los procesos de aprendizaje. En la medida en que el proceso de enseñanza y aprendizaje del conocimiento matemático con el ábaco cerrado se extiende a toda la población de la escuela se disminuye la ruptura pedagógica en las poblaciones estudiantiles que educa la escuela, fortaleciendo propuestas curriculares inclusivas entorno a (contenidos temáticos, tiempos, didácticas, evaluación, promoción escolar); y generando impacto en los proyectos educativos institucionales que le apuestan a la inclusión, en la educación para todos.
En Colombia, el Ministerio de Educación Nacional (2017) en la mirada educativa de la discapacidad visual, considera que ésta
Implica el reconocimiento de las personas ciegas o con baja visión como individuos con potencialidades, posibilidades de crecimiento y características cognitivas que se consolidan mediante la comprensión de estímulos sensoriales diferentes a los visuales, desde los cuales incorporan formas particulares de leer el mundo. (Documento de orientaciones técnicas, administrativas y pedagógicas para la atención educativa a estudiantes con discapacidad en el marco de la educación inclusiva, p. 122).
Así mismo establece para el estudiante con discapacidad visual:
Sistemas de aprendizaje como el braille (manual, a través de la plantilla braille y el punzón, o en función de apoyos tecnológicos como la máquina Perkins o la línea braille) y apoyos para otras áreas (el ábaco para la adquisición de algunos conceptos matemáticos, adaptaciones en relieve para geometría y mapas táctiles para geografía). P. 131
Para el uso del ábaco cerrado se establecen para todos los niños de la escuela, en situación o no de discapacidad visual convenciones culturales que posibilitan a los estudiantes la escritura y la lectura de cantidades, la suma “sin llevar y llevando”, la resta “sin prestar y prestando” la multiplicación, la multiplicación por varios factores, la división, los fraccionarios en forma concreta y la escritura en braille. En Colombia, el instituto nacional para ciegos INCI ha elaborado diversas cartillas que enseñan los procedimientos para elaborar estas operaciones (2000):
Los ejercicios se desarrollan de derecha a izquierda y en lo posible el procedimiento se parece al de tinta, ya que la experiencia nos ha enseñado que el lenguaje empleado por el maestro es el mismo para todos los niños, lo que nos ha llevado a modificar la ejecución de estos ejercicios para que sean similares a lo que está desarrollando el maestro en el aula de clase. Esto no quiere decir que si usted lo hace de izquierda a derecha lo esté haciendo mal lo importante en el caso del niño o niña ciego es que entienda los pasos que sigue el maestro de matemáticas cuando está realizando un ejercicio y así mismo él construya y elabore sus propios esquemas. (Introducción, p. 6).
Las operaciones aritméticas que el estudiante aprende en la básica primaria se desarrollan en lo comprendido desde el constructivismo genético como el conocimiento lógico- matemático; y éste es el que construye el niño al relacionar las experiencias obtenidas en la manipulación de los objetos; y es una abstracción reflexiva que no es producto de los objetos concretos, este conocimiento no es observable y es el niño quien lo construye en su mente a través de las relaciones con los objetos, desarrollándose siempre de lo más simple a lo más complejo, teniendo como particularidad que el conocimiento adquirido una vez procesado no se olvida, ya que la experiencia no proviene de los objetos sino de su acción sobre los mismos.
En este conocimiento matemático es pilar la construcción desde los esquemas cognitivos del estudiante el concepto de número, y que éste es un concepto lógico de naturaleza distinta al conocimiento físico o social, y se construye a través de un proceso de abstracción reflexiva de las relaciones entre los conjuntos que expresan número. Según Piaget, la formación del concepto de número es el resultado de las operaciones lógicas como la clasificación y la seriación; las operaciones mentales sólo pueden tener lugar cuando se logra la noción de la conservación, de la cantidad y la equivalencia, término a término; así como los conceptos de ordinalidad y cardinalidad.
El pensamiento lógico matemático es elaborado por cada niño, es decir, es construido desde dentro hacia fuera (en términos de cognición) y no puede ser descubierto desde el entorno o aprendido por transmisión, a excepción de los signos matemáticos. El conocimiento lógico matemático se compone de relaciones construidas por cada individuo internamente. De igual manera, el concepto de número es una síntesis de dos tipos de relaciones que el niño establece entre objetos. Una es el orden, y la otra, la inclusión jerárquica; la teoría también contrasta con la suposición habitual según la cual los números pueden enseñarse por transmisión social, pues en el conocimiento lógico matemático, la fuente última del conocimiento es el niño mismo. Según Piaget, el número es una estructura mental que construye cada niño mediante una aptitud natural para pensar, en vez de aprenderla del entorno.
Así mismo Godino (1998), autor al cual suscribimos, dice que para construir conocimientos matemáticos es preciso combinar varios factores en una secuencia de aprendizaje:
1. Es importante proponerles situaciones en las que tengan un papel activo, es decir, plantearles algo que tengan que hacer, por ejemplo: distribuir cosas entre..., buscar todos los que tengan..., construir una figura que sea..., y, a ser posible, que tengan una implicación personal en la propuesta, ya sea porque corresponda a alguna situación de la vida diaria.
2. Igualmente, es importante ofrecer material que ayude a representar la propuesta: cubos, ábacos, instrumentos de medida, cuerpo geométrico o material para construirlos, etc., es decir, algo que permita que, al pensar maneras de resolver una determinada cuestión, se pueda materializar y comprobar los resultados de una manera física.
3. La manipulación, siempre que sea posible, no debería ser silenciosa; debemos intentar que describan lo que están haciendo, que evoquen lo que hicieron en otro momento, motivarles con preguntas para que hagan conjeturas, expresen lo que están considerando y que lo discutan con sus compañeros.
4. También ayudar a generalizar, a encontrar “la norma”, para lo cual hay que promover experiencias similares que consideren un abanico de ejemplos suficientes y representativos que sirvan de referencia, y conducir, con preguntas y ejemplos, el pensamiento de los niños hasta llegar a la conceptualización.5. No hay que olvidar tampoco la importancia de la mecanización. Las matemáticas hay que comprenderlas, pero también hay que practicarlas con el fin de alcanzar un dominio que permita utilizarlas economizando esfuerzos; por lo tanto, deben proponerse también ejercicios encaminados a conseguir una automatización de determinadas habilidades.
Brousseau (1986, 1988b, 1994, 1999) en la Didáctica de la Matemática de la escuela francesa desarrolla la “Teoría de Situaciones”, que es una teoría de la enseñanza, en la cual el alumno en un proceso de acción-reflexión y desequilibrio frente al objeto de aprendizaje, y para el caso particular de la disciplina de la matemática usa los esquemas de pensamiento para aprehender y comprender los objetos matemáticos. En palabras de Brousseau (1994)
Hemos llamado situación a un modelo de interacción de un sujeto con cierto medio que determina a un conocimiento dado como el recurso del que dispone el sujeto para alcanzar o conservar en este medio un estado favorable. Algunas de estas “situaciones” requieren de la adquisición “anterior” de todos los conocimientos y esquemas necesarios, pero hay otras que ofrecen una posibilidad al sujeto para construir por sí mismo un conocimiento nuevo en un proceso “genético”.
La teoría de situaciones se enmarca en la concepción constructivista –en el sentido piagetiano- del aprendizaje, que es caracterizada por Brousseau (1986) de esta manera:
El alumno aprende adaptándose a un medio que es factor de contradicciones, de dificultades, de desequilibrios, un poco como lo hace la sociedad humana. Este saber, fruto de la adaptación del alumno, se manifiesta por respuestas nuevas que son la prueba del aprendizaje.
El aprendizaje de los estudiantes como construcción individual de la enseñanza escolar de la matemática en la teoría de las situaciones didácticas es posible en las relaciones de interacción cognitiva y verbal en la triada didáctica sujeto(s), profesor(a)-estudiantes y conocimiento; la interacción del alumno con el objeto matemático a aprender, lenguaje, operaciones, problemas y la resolución y los esquemas de pensamiento del estudiante que posibilitan o no el aprendizaje. Y la interacción del docente con el alumno en relación con ésta interacción del alumno con el aprendizaje de un conocimiento matemático particular, en dónde el docente dispone las condiciones de la matemática, las características particulares del objeto y la didáctica para la enseñanza de éste aprendizaje.
Para estas situaciones didácticas Brousseau establece la “Modelización de las Situaciones en Didáctica”, en la cual determina una clasificación de diversas situaciones didácticas: la situación de acción, la situación de formulación, la situación de validación y la situación de institucionalización. Estas situaciones didácticas muestran las interacciones alumno(s)-conocimiento matemático-profesor, en dónde el estudiante establece estrategias cognitivas y desde el saber matemático para dar respuestas y soluciones a las actividades pedagógicas y didácticas propuestas por el docente en la comprensión de que el conocimiento matemático es un saber cultural que se enseña y que se aprende.
En la situación de acción el estudiante de manera individual determina las estrategias y usa los saberes para interpretar y comprender una tarea, actividad, razonamiento, y dar una o varias soluciones a éstas. En la situación de formulación los saberes particulares de cada estudiante así como las estrategias establecidas para la resolución de la actividad de conocimiento son presentadas de forma verbal, figurativa, esquemática o en lenguaje propio de las matemáticas a otros estudiantes para establecer un diálogo de saberes que permita reconfigurar el conocimiento para la solución de la actividad entre pares, este diálogo de saberes posibilita una apertura a otras comprensiones de la tarea y otras soluciones adecuadas o menos adecuadas a la misma.
En la situación de validación los alumnos con las diferentes comprensiones de la resolución de la actividad producto de la puesta en común de las soluciones particulares, y tomando decisiones sobre las mayores certezas que dan cuenta de estas soluciones grupales establecen con los lenguajes del área de la matemática las respuestas a la actividad de conocimiento matemático, esta situación de validación hace necesaria la formalización de las respuestas encontradas a un tercero, el grupo de pares o profesor(a), quienes pueden demandar una mayor organización aceptar o confrontar las respuestas.
En la situación de institucionalización comprendida en esta interacción mencionada estudiantes-conocimiento matemático - docente, y una vez se ha realizado las confrontaciones, equilibrios y desequilibrios (en los términos piagetianos) de los estudiantes en la comprensión y solución de las tareas en la actividad establecida por el profesor(a); el profesor como actor de ésta triada didáctica y quién se constituye en el poseedor del saber cultural propio de quien enseña, es el principal responsable de la situación de institucionalización, determinando en un proceso de metacognición las soluciones presentadas por los estudiantes. El profesor sobre las respuestas construidas por los estudiantes en los momentos individual y grupal, retorna a éstos la valoración de las respuestas en los códigos y registros propios del saber disciplinar de la matemática, ésta situación de institucionalización es determinante en los procesos de enseñanza de un conocimiento formalizado y reconocido por las comunidades académicas de los saberes y conocimientos de las ciencias y potente en los procesos de aprendizaje de los estudiantes de los saberes de la cultura desde el anclaje en los propios conocimientos.
Brousseau (1994) define la situación de institucionalización, como:
La consideración “oficial” del objeto de enseñanza por parte del alumno, y del aprendizaje del alumno por parte del maestro, es un fenómeno social muy importante y una fase esencial del proceso didáctico: este doble reconocimiento constituye el objeto de la institucionalización.
Y añade también:
Debe comprenderse que la institucionalización supone establecer relaciones entre las producciones de los alumnos y el saber cultural, y no debe reducirse a una presentación del saber cultural en sí mismo desvinculado del trabajo anterior en la clase. Durante la institucionalización se deben sacar conclusiones a partir de lo producido por los alumnos, se debe recapitular, sistematizar, ordenar, vincular lo que se produjo en diferentes momentos del desarrollo de la secuencia didáctica, etc., a fin de poder establecer relaciones entre las producciones de los alumnos y el saber cultural.
El estudio se enmarca en una investigación cuantitativa, es necesario enfatizar que el “marco” teórico que se antepone a este proyecto de investigación, constituye un marco “teórico-referencial”, es decir, fuente de información y nunca modelo teórico; lo anterior dadas las condiciones de innovación de la propuesta. Esta investigación continúa las líneas abiertas de otras investigaciones de desarrollo de pensamiento lógico-matemático y operaciones de suma y resta con el ábaco abierto (Castellanos y González, 2012, 2013, 2014, 2015).
El diseño de esta investigación por su tipo y naturaleza se acomoda a un diseño cuasi- experimental de Pre-prueba _ Post-prueba con un solo grupo de control. A este grupo se le aplica una prueba previa de escritura, lectura y ejecución de números de varias cifras y de las operaciones de suma y resta en el ábaco abierto y en la representación de estas operaciones en tinta y en braille. Posteriormente se implementa la propuesta pedagógica mediada por el uso del ábaco cerrado para la escritura y lectura de números y construcción de las operaciones de multiplicación y división, para luego terminar en una prueba posterior. Las variables intervinientes son de tipo co-rrelacional en tanto que busca establecer las asociaciones y/o relaciones entre las variables ábaco cerrado y la construcción de las operaciones de multiplicación y división. El estudio se desarrolló en cinco momentos así:
En el primer momento se realiza una revisión a la propuesta pedagógica, analizando los resultados en el seguimiento y la implementación de las investigaciones con ábaco abierto desarrollados en los años 2012, 2013 y 2014 (grados pre-escolar, primero y segundo grado) en las instituciones educativas que determinan las condiciones, los grupos participantes, los docentes y se establecen los referentes de inicio para el proyecto. El seguimiento y sistematización de estas características establecen elementos de confiabilidad y validez. Al respecto de los participantes se pretende el control de la validez interna con el registro de caracterización de docentes: formación, experiencia en la profesión docente, tiempo en el curso de referencia, conocimiento previo y uso del ábaco abierto y las condiciones de aprendizaje y uso del ábaco abierto de los estudiantes matriculados en tercer grado.
En el segundo momento se realiza la evaluación de los procesos de aprendizaje de los estudiantes que ingresan a tercer grado del uso del ábaco abierto: escritura, lectura y ejecución de números de varias cifras y de las operaciones de suma y resta en el ábaco abierto y en la representación de estas operaciones en tinta y en braille. Es importante señalar que los padres informados del proyecto a desarrollar consienten la participación de los estudiantes.Esta evaluación se realiza en grupos pequeños (4-5 estudiantes) de forma ascendente en el nivel de dificultad, así primero se evalúa la ejecución con el ábaco concreto, con las cuentas, luego la representación figurativa en un dibujo del ábaco en tinta en dónde el niño dibuja las cuentas según el número solicitado y posteriormente la escritura en tinta del número, el mismo procedimiento con el niño ciego. Cuando se encuentra que el niño muestra dudas o dificultades o respuestas incorrectas en las ejecuciones, se le presenta hasta por tres veces con otros números del mismo nivel de dificultad la solicitud de la actividad, si la realiza en alguno de estos tres intentos correctamente, se continúa con la evaluación de la siguiente actividad con mayor nivel de complejidad; si en los tres intentos los resultados son incorrectos no se avanza en la prueba, sino que se inicia un nuevo proceso de enseñanza con el ábaco concreto. Como se indicó en esta prueba se evalúa hasta las operaciones de suma llevando y resta prestando con cantidades hasta de 5 dígitos.
En el tercer momento se estructura la propuesta pedagógica, en las consideraciones teóricas y prácticas de las situaciones didácticas de Brousseau (1999), elaborando las cartillas “paso a paso. Matemática preescolar”, “paso a paso. Matemáticas primero”, “paso a paso. Matemáticas segundo” y “paso a paso. Matemáticas tercero”, en cada una de ellas se elaboran las situaciones didácticas en las que se plantean procesos de aprendizaje explicitando actividades de las situaciones de acción, formulación, validación e institucionalización, los niños elaboran de manera individual, con el grupo de pares y en procesos de enseñanza didáctico con el profesor(a) los dominios culturales de la disciplina de la matemática en las propuestas curriculares para la enseñanza de la básica primaria.
En las situaciones didácticas de la cartilla paso a paso. Matemáticas tercero, las actividades se inician siempre con acciones concretas con el ábaco cerrado, el estudiante de manera individual desde los esquemas de pensamiento y de saberes previos resuelve la actividad planteada en la cartilla, correspondiendo a la situación de acción. En la situación de formulación también mostrada en la cartilla con convenciones, se solicita que ahora resuelva una actividad con los compañeros, representando la solución con el ábaco cerrado o dibujando la respuesta en dibujos del ábaco, situación de validación. En la cartilla también se indica las formas de presentación de estas soluciones concertadas o no por el grupo de estudiantes, y que corresponden al lenguaje propio de la disciplina (uso de signos y símbolos) y que permite la comprensión o cuestionamiento por todos los niños del grupo escolar.
La cartilla también establece la situación de institucionalización que es dirigida por el docente y que da cuenta de los diversos procesos de comprensión individual y de andamiaje con el grupo de pares de la actividad para el desarrollo de la actividad pedagógica particular. El profesor en la dinámica equilibrio-desequilibrio cognitivo del estudiante apalanca una reconceptualización de la actividad; posterior a esta interacción docente-conocimiento-estudiante(s) el estudiante revisa la actividad desarrollada.En el cuarto momento, la implementación de la propuesta pedagógica en el uso del Ábaco cerrado y utilizando la cartilla paso a paso. Matemática de tercero, se realiza un proceso de capacitación a docentes y padres de familia de los estudiantes de tercer grado sobre el uso del ábaco en la escritura y lectura de cantidades y la realización de las operaciones de multiplicación y división. Esta capacitación es desarrollada por los investigadores, un profesor experto en el uso del ábaco cerrado y los estudiantes principiantes de investigación (EPI) del programa de licenciatura en Pedagogía Infantil.
En el quinto y último momento cuando se ha desarrollado en el año lectivo y correspondiente con los lineamientos curriculares en el área numérica de la matemática las situaciones didácticas de la cartilla se realiza la prueba de evaluación de la escritura, lectura y ejecución de números de varias cifras y de las operaciones de multiplicación y división en el ábaco cerrado y en la representación de estas operaciones en tinta y en braille. Es importante señalar que igual que la evaluación inicial, esta segunda evaluación-post se realiza en grupos pequeños (4-5 estudiantes) y de forma ascendente en el nivel de dificultad, así primero se evalúa la ejecución con el ábaco cerrado concreto, con las cuentas, luego la representación figurativa en un dibujo del ábaco en tinta en dónde el niño dibuja las cuentas según el número solicitado y posteriormente la escritura en tinta del número, y las operaciones, también se realiza el mismo procedimiento con el niño ciego, que permite determinar la correlación entre ábaco cerrado y construcción de las operaciones de multiplicación y división.
Los participantes del estudio, fueron 120 niñ@s que durante el año 2015 cursaron el grado tercero de la educación básica primaria en la institución educativa Alberto Lleras Camargo en la cual el Proyecto Educativo Institucional (PEI) tiene un enfoque inclusivo, en las sedes: Betty Camacho de Rangel, Camelias, Cataluña, y Narciso Matus Torres de la ciudad de Villavicencio (Meta) en Colombia. En el grupo de niños un estudiante presenta discapacidad visual.
La comunidad de práctica que participó en este estudio se conformó con 12 docentes de grado Tercero, 16 padres de familia, El estudio fue desarrollado por 2 investigadoras, 1 experto en enseñanza con el ábaco y 6 estudiantes principiantes de investigación (EPI) de la Universidad de los Llanos, quienes durante su práctica docente desarrollaron las sesiones de enseñanza.
El ábaco cerrado como mediación pedagógica en la construcción de las operaciones de multiplicación y división en el grado tercero de instituciones educativas oficialesSe presentan diversas figuras de las actividades realizadas por los niños en las situaciones de acción, formalización, validación e institucionalización:
Figura 1. Cartilla Paso a paso. Tercero

Esta actividad de situación de institucionalización es resuelta por el niño, inicia con la realización en el ábaco cerrado (objeto concreto) y posteriormente es representado figurativamente en el dibujo en la cartilla del ábaco, se confronta con la valoración (institucionalización) y correcta respuesta por el profesor. En la segunda respuesta hay un error en la escritura de las centenas.
Figura 2. Cartilla Paso a paso. Tercero
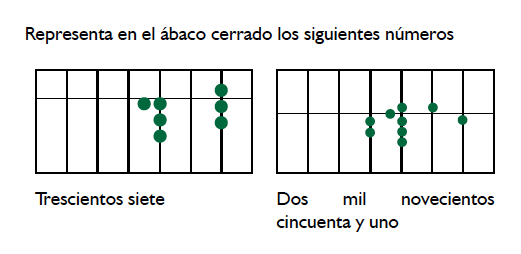
Esta actividad de situación de institucionalización es resuelta por el niño, inicia con la realización en el ábaco cerrado (objeto concreto), es determinante para la respuesta en la cartilla, que el dibujo del ábaco cerrado muestre claramente el bastidor, las varillas y los puntos de relieve que representa el punto de mil, millón, la coma decimal entre otros, para un total de 6 puntos que se enumeran de derecha a izquierda. Se confronta con la valoración (institucionalización) y correcta respuesta por el profesor. En la respuesta hay un error en la escritura de las cantidades en la figura del ábaco y en la escritura en tinta.
Figura 3. Cartilla Paso a paso. Tercero
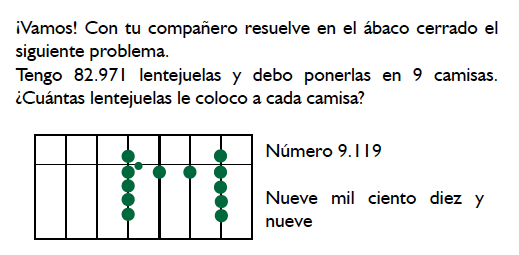
Con un ábaco cerrado resuelve el siguiente problema de multiplicación y escribe el resultado con números y con letras. En una distribuidora de agua potable salen 25.888 botellas diarias para la venta. ¿Cuántas botellas de agua se venden en 8 días?
Esta última actividad de formalización, es resuelta en lenguaje propio de las matemáticas con un par en la que se propicia una comprensión desde las particulares cognitivas de cada estudiante para una reconceptualización de la operación aritmética. Para cada temática de la aritmética de tercer grado de la Básica primaria se elaboraron las unidades didácticas con las situaciones didácticas señalas por Brousseau. Las cuales se resolvieron individualmente por los estudiantes, por grupos de estudiantes y con la reconceptualización cognitiva y de veracidad de las respuestas por el profesor.La evaluación (evaluación post) al desarrollo de las unidades de la cartilla Paso a paso. Tercero se realizó en grupos de niños con respuestas individuales en los que se encontró que el total de los estudiantes realizan con el ábaco cerrado concreto la escritura de cantidades hasta 9 dígitos con cero intermedio y cero final, también la totalidad de los niños (120) realizan en los dibujos del ábaco cerrado la representación correcta de escritura y lectura de cantidades, así como las operaciones de suma y resta. El 100% de los niños realizan correctamente la multiplicación con cantidades de hasta 8 dígitos sin ceros y el 90% la multiplicación con cantidades de 8 dígitos con cero(s) intermedios. También el 90% de los niñ@s realizan correctamente la división con cantidades de 6 dígitos con y sin cero intermedios. Estas últimas operaciones de multiplicación y división con ábaco cerrado concreto, representación figurativa y escritura de símbolos propios del lenguaje matemático.
El ábaco cerrado es una mediación pedagógica importante en los procesos de escolarización en la construcción del pensamiento matemático de los niños en la educación básica primaria, es una mediación que posibilita un proceso de construcción cognoscitiva de los estudiantes de las operaciones aritméticas de multiplicación y división, en espacios de inclusión como un derecho de los niños a aprender en una escuela para todos.
Se encuentra una correlación positiva entre el uso del ábaco cerrado y el aprendizaje de las operaciones de multiplicación y división en el grado tercero de las instituciones educativas del estudio, con estudiantes con y sin discapacidad visual por su posibilidad de ser un objeto concreto que se puede manipular para la comprensión del valor posicional que es el sistema de base 10 y posterior representación figurativa y simbólica y que se establece para la enseñanza de la matemática en los lineamientos curriculares de la educación básica primaria en Colombia.
Las situaciones didácticas propuestas por Brousseau (1999): la situación de acción, la situación de formulación, la situación de validación y la situación de institucionalización, presentan la importancia en la situación didáctica de las interacciones alumno(s)-conocimiento matemático-profesor, desde las construcciones individuales de cada estudiante, el equilibrio-desequilibrio y nuevo equilibrio en espiral del aprendizaje con otros y la recognición del profesor de este conocimiento matemático; se constituyeron en rutas cognoscitivas didácticas en las actividades de las unidades didácticas de la cartilla Paso a paso. Tercero. El estudiante con discapacidad muestra dominio y competencia en cada una de estas situaciones didácticas.
El estudio muestra la importancia de la enseñanza de la matemática como construcción individual del estudiante con mediaciones de material concreto, y en contra de la enseñanza de la matemática desde la oralidad y la representación formalizada de la aritmética sin atender las características de la disciplina y las condiciones cognitivas de quien aprende. Este estudio también muestra la importancia de que en las instituciones formadoras de licenciados en educación infantil y en básica primaria se reflexione en las didácticas para la enseñanza en la educación infantil y grados de la educación básica a los niños y las niñas con y sin discapacidad visual en el conocimiento cultural de la matemática.
Los profesores directores de los cursos y los padres de los estudiantes del estudio, en la vivencia de la construcción del conocimiento matemático con el ábaco cerrado, encuentran la importancia del valor posicional, así como los conceptos de ordinalidad y cardinalidad para la enseñanza por los profesores y el acompañamiento en las tareas por los padres como determinantes en el aprendizaje de los niños y el uso de estos aprendizajes escolares en la cotidianidad del estudiante.
Las bondades del uso del ábaco abierto en la enseñanza y el aprendizaje de las operaciones de adición y resta y del ábaco cerrado en las operaciones de multiplicación y división por parte de los estudiantes se muestran en relación directa con la comprensión y el dominio por parte del profesor del ábaco, así como de la profunda comprensión de los procesos de pensamiento matemático del estudiante.
Andrade, C. (2011) Obstáculos didácticos en el aprendizaje de la matemática y la formación de docentes. Comité Latinoamericano de Matemática Educativa. Capítulo 4. El pensamiento del profesor, sus prácticas y elementos para su formación profesional. Disponible en http://funes.uniandes.edu.co/5056/1/EscobarObst%C3%A1culosALME2011.pdf
Arteaga, B., Macías, J., Núñez del Río, C. (2016). Aprender con el ábaco japonés. Matemáticas, y… ¿algo más? XVI Congreso Nacional y VII Congreso Iberoamericano de Pedagogía: Democracia y Educación en el Siglo XXI. Sociedad Española de Pedagogía. Madrid, 28-30. [Versión PDF] disponible en https://researchgate.net/.../301200489_Aprender_con_el_ábaco_japonés_Matemáticas
Barody, A.J. (1988). El pensamiento matemático de los niños. Madrid. Visor-M.E.C.
Barros, F. (2008). Enseñanza de las ciencias desde una mirada de la didáctica de la escuela francesa. Revista Escuela de Ingeniería de Antioquia, Medellín (Colombia). Número 10, p. 55-71. Diciembre 2008. Disponible en https://dialnet.uniroja.es/descarga/ articulo/2968038.pdf
Brousseau, Guy (2007). Iniciación al estudio de la teoría de las situaciones didácticas. Buenos Aires: Editorial Zorzal
Brousseau, G. (1986). Fundamentos y métodos de la Didáctica de la Matemática. Universidad Nacional de Córdoba, Facultad de Matemática Astronomía y Física, Serie B, Trabajos de Matemática, No. 19 (versión castellana 1993)
Brousseau G. (1994). Los diferentes roles del maestro. En Didáctica de Matemáticas. Aportes y reflexiones, C. Parra; I. Saiz (comp.) Buenos Aires, Paidós Educador.
Castellanos, M., González, O. (2015). Operaciones lógicas y procesos de pensamiento matemático en el pre-escolar. Actas JAEM. 17 Jornadas para el aprendizaje y la enseñanza de las matemáticas.
Chavarría, J. (2006).Teoría de las situaciones didácticas. Cuadernos de investigación y formación en educación matemática, 1(2). Disponible en https://revistas.ucr.ac.cr/index.php/cifem/article/View/6885
DAmore, B., Fandiño, M. (2015). Propuestas metodológicas que constituyeron ilusiones en el proceso de enseñanza de la matemática. Vol. 27, N°3, pp. 7-43. Grupo Santillana México. Distrito Federal. [Versión PDF] disponible en http://www.redalyc.org/artículo. oa?id=40544202001
Dickson, L., Brown, M., Gibson, O. (1991). El aprendizaje de las Matemáticas. Barcelona. Editorial Labor, S.A. Flavel, J. H. (1982). La psicología evolutiva de J. Piaget. Barcelona. Paidós.
Furth H. (1978). La teoría de Piaget en la práctica. Buenos Aires. Kapeluz.
Godino, Juan D. (1998) Matemáticas y su didáctica para maestros. Fundamentos de la enseñanza y el aprendizaje de las matemáticas para maestros. Universidad de Granada. Facultad de Ciencias de la Educación. Disponible en: [ http://www.ugr.es/local/jgodino/ edumat-maestros/]
Instituto Nacional de Ciegos. INCI. (2009). Orientaciones pedagógicas para la atención educativa a estudiantes con limitación visual. Guía n° 17. Colombia
León-Pinzón, N., Medina-Sepúlveda, M. (2016). Estrategia metodológica para el desarrollo del pensamiento lógico matemático en niños y niñas de cinco años en aulas regulares y de inclusión. Revista Inclusión & desarrollo, 3 (2), 35-45. Disponible en http://biblioteca.uniminuto.edu/ojs/index.php/|YD/issue/archive
Lovell, K. (1986). Desarrollo de los conceptos básicos matemáticos y científicos en los niños. Madrid. Morata.
Madrid, H. Pablo., Rosa, A. (2003). Congreso estatal sobre prestación de servicios para personas ciegas y deficientes visuales. Colombia.
Maldonado, J., Francia, A. (1996). Desarrollo del pensamiento lógico-matemático en la edad preescolar. Manual para maestros. Universidad Pedagógica Experimental Libertador. Maracay (Venezuela)
Marchesi, Á., Tedesco, J. C., Coll, C. (2012). Calidad, equidad y reformas en la enseñanza. Madrid (España) Santillana. Colección Reformas educativas. Metas Educativas 2021.Ministerio de Educación Nacional (2017). Documento de orientaciones técnicas, administrativas y pedagógicas para la atención educativa a estudiantes con discapacidad en el marco de la educación inclusiva. Bogotá (Colombia)
Ministerio de Educación Nacional (1998). Lineamientos curriculares en matemáticas. Cooperativa Editorial Magisterio. Bogotá (Colombia)
Ministerio de Educación Nacional (2002). Estándares para la excelencia en la educación. Estándares curriculares para las áreas de matemáticas, lengua castellana y ciencias naturales y educación ambiental para la educación preescolar, básica y media. Bogotá (Colombia). Cooperativa Editorial Magisterio.
Ministerio de Educación Nacional de Colombia –MEN. (1997b). [versión PDF]. Recuperado de http://www.mineducacion.gov. co/1621/articles-89869_archivo_pdf10.pdf
Pachón, N., Parada, A., Chaparro, Z., (2016). El razonamiento como eje transversal en la construcción del pensamiento lógico. Praxis & Saber, 7 (4), pp. 219-243.
Palacios, J.; Marchesi, A. y Coll, C. (1994). Desarrollo Psicológico y Educación. Madrid (España). Alianza Editorial.
Piaget, J., Inhelder. (1983). Génesis de las estructuras lógicas elementales. Buenos Aires: Editorial Guadalupe. Piaget, J., Szeminska, A. (1987). Génesis del número en el niño. Buenos Aires (Argentina). Editorial Guadalupe. Piaget, J. (1987). Introducción a la epistemología genética. El pensamiento matemático. México. Paidós.
Quiñones, M., Rodríguez, M., Piña, C. (xxx). Las situaciones (Didácticas) de formación matemática o las competencias del saber “enseñado”. XIV Congreso de enseñanza y aprendizaje de las matemáticas. Diversidad y Matemáticas. Sociedad Andaluza de Educación Matemática THALES. Disponible en https://thales.cica.es/xivceam/actas/pdf/com04.pdf.
Rico, L., Castro, E. (1987). Fundamentos para una Aritmética Escolar. Madrid. Editorial Síntesis.